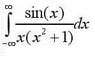You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Help Solving Integral: pi*(1-1/e)
- Thread starter gholamghar
- Start date
-
- Tags
- Integral
Physics news on Phys.org
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
How about showing us HOW you got that result? I think I would be inclined to integrate around a loop in the complex plane- integrate from -R to R on the real line, then counter-clockwise around the half circle in the positive i half plane with radius R. The function has a pole at z= i. (And a removable discontinuity at z= 0.) Then, of course, take the limit as R goes to infinity. Since the integrand obviously goes to 0 as |z| goes to infinity, the integral depends completely on the residue at z= 1. Did you calculate the residue?
But that might be exactly what you are trying to do or it might be completely different. What, if anything, you did wrong, we can't say until we see what you did.
And since this does not have anything, directly, to do with "differential equations", I am moving it to "Calculus and Analysis".
Last edited by a moderator:
gholamghar
- 23
- 0
thanks for the answer,it helped a lot
Similar threads
- Replies
- 2
- Views
- 3K
- Replies
- 29
- Views
- 4K
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 5
- Views
- 1K
- Replies
- 16
- Views
- 2K
- Replies
- 8
- Views
- 3K
- Replies
- 12
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 2K
Hot Threads
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 18
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math