- #1
anhnha
- 181
- 1
Hi,
I want to ask one question about wavelength. Here is a picture defining wavelength.
To get a sinusoidal wave in space, we have to use a sinusoidal voltage source at transmitter, right?
I mean if there is a sinusoidal voltage source at the transmitter to create a sinusoidal wave in space.
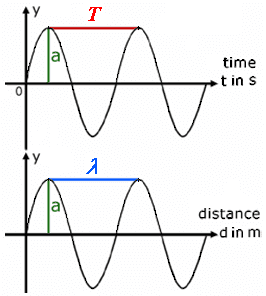
I want to ask one question about wavelength. Here is a picture defining wavelength.
To get a sinusoidal wave in space, we have to use a sinusoidal voltage source at transmitter, right?
I mean if there is a sinusoidal voltage source at the transmitter to create a sinusoidal wave in space.
