- #1
asdf12312
- 199
- 1
help understanding magnitude and phase of sinc functions??
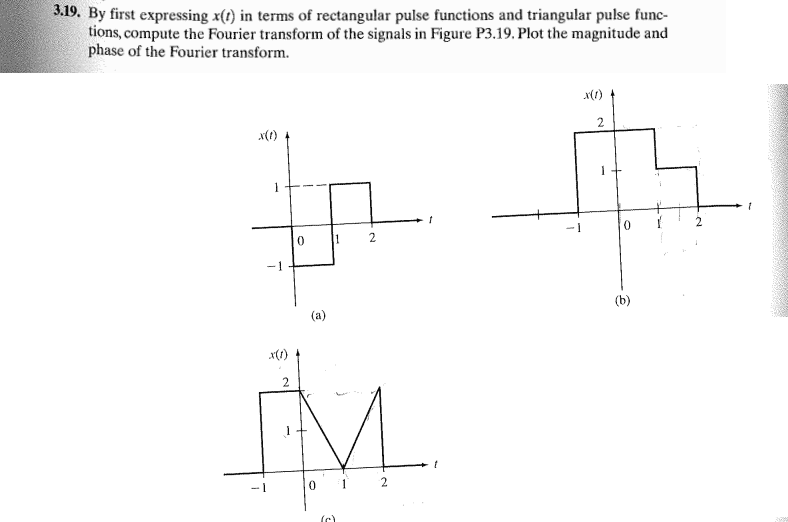
pτ(t) ⇔ τsinc([itex]\frac{τω}{2\pi}[/itex])
Δτ(t) ⇔ [itex]\frac{τ}{2}[/itex]sinc2([itex]\frac{τω}{4\pi}[/itex])
sinc(x) = [itex]\frac{sin(\pi x)}{\pi x}[/itex]
My instructor had posted solutions to the problems:
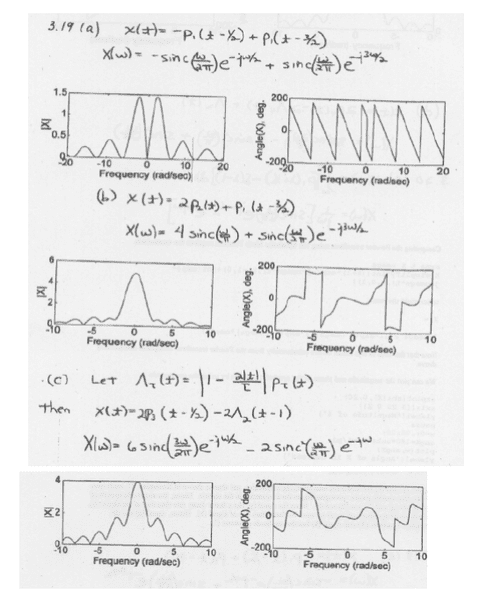
I understand how to get the Fourier transforms, I was just having problems finding magnitude and phase graphs. For a) I don't know how they got amplitude near 1.5, but I know that in general for a single sinc function sinc(x), you will have zeroes at x-1. I also know that in general phase graphs of single sinc function will be +180 deg (doesnt really matter what the sign is, I guess) when you have zeroes. I just don't understand how this works when there are multiple sinc or sinc2 functions. And why the phase graphs are all sawtooth etc., when I was expecting just + 180deg.
Homework Statement
Homework Equations
pτ(t) ⇔ τsinc([itex]\frac{τω}{2\pi}[/itex])
Δτ(t) ⇔ [itex]\frac{τ}{2}[/itex]sinc2([itex]\frac{τω}{4\pi}[/itex])
sinc(x) = [itex]\frac{sin(\pi x)}{\pi x}[/itex]
The Attempt at a Solution
My instructor had posted solutions to the problems:
I understand how to get the Fourier transforms, I was just having problems finding magnitude and phase graphs. For a) I don't know how they got amplitude near 1.5, but I know that in general for a single sinc function sinc(x), you will have zeroes at x-1. I also know that in general phase graphs of single sinc function will be +180 deg (doesnt really matter what the sign is, I guess) when you have zeroes. I just don't understand how this works when there are multiple sinc or sinc2 functions. And why the phase graphs are all sawtooth etc., when I was expecting just + 180deg.
Last edited: