ehild said:
Σ
When writing up the equation for the acceleration, you need to take also the tension in the strings into account.
Write the equation as mdv/dt=ΣF, use the relation given between v and x, and see what you get. Show your work.
There's has been a lot of debate on this thread about this solution, and I think there have been a number of mistakes made, so I wanted to chime in and (hopefully) clarify things.
First, a couple of points:
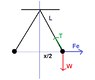
1) The tension on the rope is always perpendicular to the motion of the spheres, and thus plays no direct role on their motions. It is possible to write your equations in such a way that the tension does not appear, which makes all of the math simpler.
2) The question asks us to assume that the distance between the spheres is far smaller than their connecting point. This is another way of saying that we can safely ignore the fact that the spheres move in a circle: we can consider it to just be two spheres moving horizontally towards one another. This means that gravity plays no role.
3) The problem is asking us to match up an equation of motion (##v = a/\sqrt{x}##) with a force magnitude (related to the dissipation of charge). The concept of equilibrium plays no role, because the relationship between force and acceleration acts both in and out of equilibrium.
The way I would approach this problem is as follows:
1) Write down the equation for the relative distance between the spheres. This is a function for v(t) given x(t), i.e. a differential equation. It should be solvable to provide an equation x(t).
2) Write down the equation for the electrostatic force between the spheres. This is a function of F(t) given v(t) and q(t). You could use ##\vec{F} = m\vec{a}## to solve for q(t). Note that the problem structure has one-dimensional motion, so we don't need to worry about any vector sums, except for getting the signs right on the equations.
I haven't solved the problem, but one general comment I have is:
Try keeping everything in terms of differential equations as long as possible, to see if you can simplify things. Getting a picture of the whole problem may provide hints with ways to make your life easier. It may not be necessary to solve the differential equation for v(t) given x(t) at all. If that doesn't seem simpler, just solve the differential equation for x(t), which will make the equation for q(t) a matter of algebra.
 .
. 
 .
.