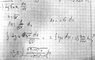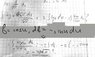Help with IntegralS Very Important Quick

[Hootenanny]

U know... I know that. I don`t know how to do that! =(

Don't let yourself get stressed out when your answering questions, after all they're only questions. Take a look at the first line in one of my previous posts;

x = 2\sin(u) \Rightarrow dx = 2\cos(u) \; du

Does this give you any ideas?

 

[Student from UA]

sin(u)=x/2
u=((-1)^n)arcsin(x/2) + Pi n, n E Z

 

[Hootenanny]

sin(u)=x/2
u=((-1)^n)arcsin(x/2) + Pi n, n E Z

Your almost correct, but aren't you forgetting one 'little' thing...? I'm impressed at how your represent your solution, not many students would think of representing it this way; in truth it is not normally scary unless the question explicitly requires it.

 

[Gib Z]

I don't understand why you think that. Good to notice you've learned latex so fast.
\sin u = \frac{x}{2}
\arcsin (\sin u) = \arcsin (x/2)
u=\arcsin \frac{x}{2}

I see why you wrote it that way, but it over complicates the situation this time. Quite Interesting though...

EDIT: In fact it destroys you in this case...The pi*n term gets included in the constant term, and then the integral becomes (-1)^n \arcsin (x/2) + C, and that is incorrect...

 

[Student from UA]

I start do 6th and.. have problems in middle. see in atach

 

[Student from UA]

so the rsult of 5: \intdu=\arcsin \frac{x}{2} + C ?

 

[Gib Z]

I have no idea what the "tg" is, but I deduce its the tangent function.

Even if it isnt, let u=\sqrt{x} Then \frac{du}{dx} = \frac{1}{2u}, dx = 2u du

so the integral becomes

\int \tg u \frac{2u}{u} du = 2\int \tg (u) du

EDIT: As to post 36, q5, yes that is the answer. The reason you can not write it as you did previously is because it is only valid for n E Z, but we need it to be valid for all real values of n.

 

[Student from UA]

Gibs u=\sqrt{x}
du=\frac{1}{2\sqrt{x}}dx then dx=2\sqrt{x}du

 

[Gib Z]

Check your typing, you forgot to use the right hand brace } instead of right breacket ). Anyway, then you are correct. However, didn't we say u=\sqrt{x}?

 

[Gib Z]

You know either way it doesn't matter. You are stuck with
2\int \frac{\sin x}{\cos x} dx which can be solved by letting u = cos x

 

[Student from UA]

right result?

 

[Gib Z]

Nope.

2\int \frac{\sin x}{\cos x} dx
let u = cos x, then du = - sin x dx
-2\int \frac{1}{u} du = -2\log_e u + C = -2 \log_e (\cos x) + C

 

[Student from UA]

Nope.

2\int \frac{\sin x}{\cos x} dx
let u = cos x, then du = - sin x dx
-2\int \frac{1}{u} du = -2\log_e u + C = -2 \log_e (\cos x) + C

U right, i agree with u. I made a child mistake =(
simply I sit near computer and do homework already 6 hours and have square head

 

[Student from UA]

start the 7th. Stop in the middle. See in atach. :zzz:

 

[cristo]

So you have the integral of sec u= 1/cos u. To compute this, try multiplying top and bottom by sec u+tan u.

 

[Student from UA]

i don`t understand u cristo =(

 

[Student from UA]

stop don`t tell me anything 5 minut i try tio solve it again.

 

[Student from UA]

secu^2= 1+tgu^2 => secu=sqrt(1+tgu^2)
so compare 3rd step and last in atach . hmm

 

[cristo]

\sec u=\sec u\cdot\left(\frac{\sec u+\tan u}{\sec u+\tan u}\right). Can you integrate this?

[Hint: How is the numerator related to the denominator?]

 

[Student from UA]

ou... sorry =) how to delete... -) it`s mistake

 

[Student from UA]

to cristo... no i can`t =*(

 

[cristo]

Ok.. expand tp give \sec u=\sec u\cdot\left(\frac{\sec u+\tan u}{\sec u+\tan u}\right)=\frac{\sec^2u+\tan u\sec u}{\sec u+\tan u}. You worked out that d/du(tan u)=sec^2u. It can also be shown that d/du(sec u)=tan u.sec u, and thus the numerator is the exact derivative of the denominator.

Do you know how to integrate a function of the form \frac{f'(u)}{f(u)}? [Hint: Think of the most simple function of this form; namely 1/x].

 

[Student from UA]

half of your text i can`t understand. and the f`(u)/f(u) i don`t know maybe =( and i `m really tied =(

 

[Student from UA]

and id look to all that u sad ... i can`t stand =( really. can u write all step by step to result? maybe if i look i can stand

 

[Hootenanny]

If you're really tired, you should take a break; you're going to gain very little from working when your exhausted. With respect to cristo's suggestion a full proof can be found at http://math2.org/math/integrals/more/sec.htm .

 

[Student from UA]

Hootenanny: all were well if not one but. Tommorow i need to go to university with complete homework... and now i haven`t free time for relax =( head is been ill but i try to solve this stupid integrals... And it very hard to me (little ukrainian boy) study integrals on english and speak with u becouse my English not well...maybe bad.

 

[Student from UA]

ur tan it`s my tg? tangens? or what?

 

[Student from UA]

tan=sin/cos? if yes - tan it`s tg

 

[Hootenanny]

Still, not handing in homework on time isn't the end of the world and if you have been ill, I'm sure you can apply for special circumstances. However, I understand that it must be difficult for you to communicate on a predominantly english speaking forum; at least its mathematics homework your doing at not english/ukrainian

And yes, tan is our tangent (your tg) function.

 

[Student from UA]

hm... I am my situationi it`s tne end of world, becouse my my scholarship depends on it. It`s really hard to understand.. =(
Their does not interest, was ill I or no. Simply, it is necessary to give homework in time.
Please help me =( U`re my last chans half homework we do...