Another
- 104
- 5
<< Mentor Note -- OP has been reminded to use the Homework Help Template when posting schoolwork questions >>

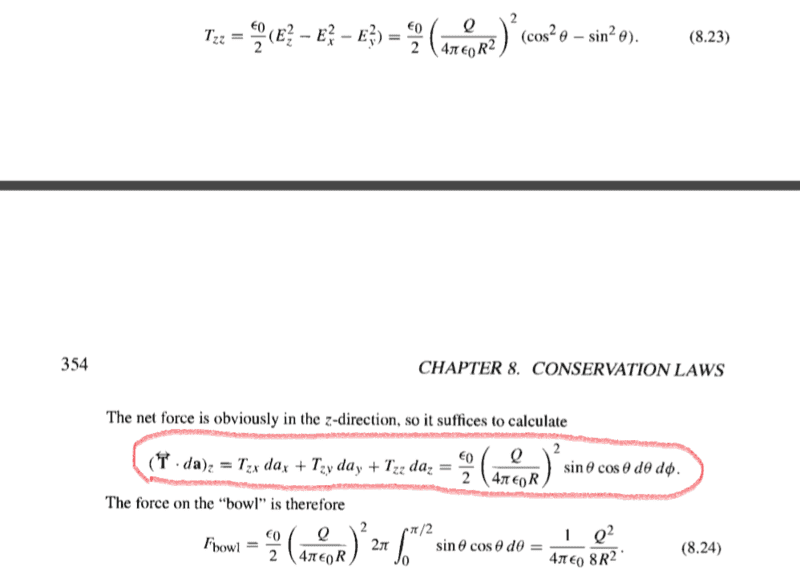
my think
if ## \hat{r} = \sin(θ) \cos( φ) \hat{x} +\sin(θ) \sin( φ) \hat{y} +\cos(θ) \hat{z} ##
## da = R^2 \sin(θ) dθdφ \hat{r} = da_{x} \hat{x} + da_{x} \hat{y} + da_{z} \hat{z}##
So
##da_{x} = R^2 \sin^2(θ) \cos(φ) dθdφ ##
##da_{y} = R^2 \sin^2(θ) \sin(φ) dθdφ ##
##da_{z} = R^2 \sin(θ) \cos(θ) dθdφ ##
where
## \int_{0}^{2π} \cos(φ) \,dφ =\int_{0}^{2π} \sin(φ) \,dφ = 0 ##
##\overleftrightarrow{T} ⋅ da = 0 + 0 + T_{zz} ⋅ da_{z} ##
##T_{zz} ⋅ da_{z} = \frac{ε_{0}}{2} \left(\frac{Q}{4πε_{o}R^2}\right)^2(\cos^2(θ) - \sin^2(θ)) ⋅ R^2\sin(θ) \cos(θ) dθdφ##
But why in textbook give by
## \frac{ε_{0}}{2} \left(\frac{Q}{4πε_{o}R^2}\right)^2 ⋅ R^2\sin(θ) \cos(θ) dθdφ = \frac{ε_{0}}{2} \left(\frac{Q}{4πε_{o}R}\right)^2\sin(θ) \cos(θ) dθdφ##
where are ##(\cos^2(θ) - \sin^2(θ))## ?. ##(\cos^2(θ) - \sin^2(θ))## is missing .
I don't understand
my think
if ## \hat{r} = \sin(θ) \cos( φ) \hat{x} +\sin(θ) \sin( φ) \hat{y} +\cos(θ) \hat{z} ##
## da = R^2 \sin(θ) dθdφ \hat{r} = da_{x} \hat{x} + da_{x} \hat{y} + da_{z} \hat{z}##
So
##da_{x} = R^2 \sin^2(θ) \cos(φ) dθdφ ##
##da_{y} = R^2 \sin^2(θ) \sin(φ) dθdφ ##
##da_{z} = R^2 \sin(θ) \cos(θ) dθdφ ##
where
## \int_{0}^{2π} \cos(φ) \,dφ =\int_{0}^{2π} \sin(φ) \,dφ = 0 ##
##\overleftrightarrow{T} ⋅ da = 0 + 0 + T_{zz} ⋅ da_{z} ##
##T_{zz} ⋅ da_{z} = \frac{ε_{0}}{2} \left(\frac{Q}{4πε_{o}R^2}\right)^2(\cos^2(θ) - \sin^2(θ)) ⋅ R^2\sin(θ) \cos(θ) dθdφ##
But why in textbook give by
## \frac{ε_{0}}{2} \left(\frac{Q}{4πε_{o}R^2}\right)^2 ⋅ R^2\sin(θ) \cos(θ) dθdφ = \frac{ε_{0}}{2} \left(\frac{Q}{4πε_{o}R}\right)^2\sin(θ) \cos(θ) dθdφ##
where are ##(\cos^2(θ) - \sin^2(θ))## ?. ##(\cos^2(θ) - \sin^2(θ))## is missing .
I don't understand

