Help with thermodynamic potentials

[Feynmanfan]

Dear friends,

I’m having trouble with this thermodynamic problem. I apologise if you don’t understand my poor English (I’m writing to you from Spain!)

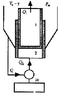
We’ve got two cylinders (1 is adiabatically isolated from 2 but not from the outside, where Pressure P and Tº are constant) and cylinder 1 can move inside cylinder 2. Cylinder 2 is isolated from the outside but it is connected to a heat pump
Suppose both cylinders contain IDEAL GAS.
Everything is in equilibrium but now we lower Tº and make it (T-C).Therefore Q1 heat will be delivered from cylinder 1. As said, Cylinder 2 is connected to a Carnot HEAT PUMP (that is maximum efficiency) and we use Q1 to heat up cylinder 2.

I need to calculate the volume of the gas in cylinder 2, entropy change in both systems and many other things I don’t want to bore you with.

Does this problem have to do with thermodynamic potentials? I’d be very grateful if you could help me.

 

[so-crates]

Cylinder 2 contains Cylinder 1, or is it a separate container?

 

[Feynmanfan]

Yes, cylinder 2 contains cylinder 1. cylinder 1 can move in cylinder 2, that is, if the gas in cylinder 2 expands, then cylinder 1 moves it's position. However, cylinder 2 is adiabatically isolated with respect to cylinder 1.

 

[so-crates]

OK then why the need for two "cylinders". Don't you just have one cylidner, with two chambers ?

Let me see if I can restate your problem

You have a cylinder of gas that is partitioned into two chambers by an adiabatic (no heat exchange ) piston. At one end of the cylinder, changes are both isothermal and isobaric (constant pressure). The other end of the cylinder is closed.

Well if one pressure and temperature cannot change in one of the cylinders, then neither can molar volume so no work can be done!

 

[Feynmanfan]

I don't think it's that easy. There's heat transfer between gas in cylinder 1 and the outside (because we've lowered the outside T) all this heat is used (through a carnot heat pump and work source) to heat up cylinder 2.

Cylinder 1 is inside cylinder 2 and you can take it out of it if you want. This doesn't mean that we have a single cylinder partitioned by a piston. And I forgot to tell you about the work source that works along the Carnot heat pump in order to transfer all the heat from the process mentioned in cylinder 1 to cylinder 2.

Thanks for your help

 

[so-crates]

So cylinder 2 can be heated from the outside. If cylinder 2 is rigid then its pressure must change and not be the same as the external pressure.

You need to know how much heat has been transferred by the heat pump, or at least what the initial and final temperatures are of cylinder 2. Are any of these given?

 

[Feynmanfan]

I know it's hard to understand the problem. No initial values are given. I only know that at first everything is in equilibrium. Then we lower the temperature and everything starts. It's the same ideal gas in both cylinders.
In the picture I can see the heat pump next to a work source (don't know what it is) Q1 (from cylinder1+outside) and W enter the pump to give Q2, which enters cylinder2.

 

[so-crates]

OK if no initial values are given, they want you to express the volume of the gas and the entropy change in terms of the change in temperature in cylinder 1, or what ?

 

[Feynmanfan]

Exactly. You can name V1, V2 etc. all initial values, knowing that everything is in equilibrium, until you change the temperature source.

 

[so-crates]

I'm still confused. If you were to post a diagram somehow it would really help out.

 

[Feynmanfan]

Diagram

See if this diagram makes it clearer.

Thanks for your interest. I hope you can help me out of this. I have to give it tomorrow.