Nanyang
- 33
- 0
[Solved] Wheel touching a kerb just about to lift. What are the forces on the wheel?
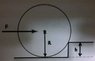
In order to lift a wheel over a kerb of height h, a minimum force F is be applied at the axle. The radius of the wheel is R. Draw all the forces on the wheel then find its weight.
*IMAGE003*
T = r X F
I managed to find the weight of the wheel. But what I am confused about is the drawing of the forces on the wheel.
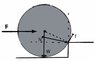
My teacher presented a drawing like this below.
f is the tangential friction on the wheel.
F is the horizontal force at the axle.
W is the weight of the wheel.
N is the normal reaction force at the point of contact.
*IMAGE003a*
Since he argued that without friction the wheel will slide and therefore the wheel cannot be pushed up the kerb. Thus we must conclude that the normal reaction force on the point of contact is not passing through the center of the wheel, otherwise that point will move.
However I do not understand. Because if we imagine the surface of the point of contact is an infinitesimally flat surface, and the friction is parallel to the surface but the normal reaction force would be perpendicular to the surface. Therefore N would pass through the center for geometrical reasons.
However this is a dilemma. Since if there is friction then that point of contact will move. So I must conclude that there is no friction present. In other words, since there is no force parallel to that surface in contact, there cannot be any static friction.
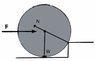
So instead my drawing is like below.
*IMAGE003b*
Which is correct? My teacher gave an example of the situation on an ice kerb. He says that it will otherwise be impossible for the wheel to be lifted up by the horizontal force. However, I feel that even if there is no friction it is possible for the wheel to be lifted up the kerb.
Both drawings give the same answer to the weight of the wheel since it is done by taking the torque relative to the point of contact.
Homework Statement
In order to lift a wheel over a kerb of height h, a minimum force F is be applied at the axle. The radius of the wheel is R. Draw all the forces on the wheel then find its weight.
*IMAGE003*
Homework Equations
T = r X F
The Attempt at a Solution
I managed to find the weight of the wheel. But what I am confused about is the drawing of the forces on the wheel.
My teacher presented a drawing like this below.
f is the tangential friction on the wheel.
F is the horizontal force at the axle.
W is the weight of the wheel.
N is the normal reaction force at the point of contact.
*IMAGE003a*
Since he argued that without friction the wheel will slide and therefore the wheel cannot be pushed up the kerb. Thus we must conclude that the normal reaction force on the point of contact is not passing through the center of the wheel, otherwise that point will move.
However I do not understand. Because if we imagine the surface of the point of contact is an infinitesimally flat surface, and the friction is parallel to the surface but the normal reaction force would be perpendicular to the surface. Therefore N would pass through the center for geometrical reasons.
However this is a dilemma. Since if there is friction then that point of contact will move. So I must conclude that there is no friction present. In other words, since there is no force parallel to that surface in contact, there cannot be any static friction.
So instead my drawing is like below.
*IMAGE003b*
Which is correct? My teacher gave an example of the situation on an ice kerb. He says that it will otherwise be impossible for the wheel to be lifted up by the horizontal force. However, I feel that even if there is no friction it is possible for the wheel to be lifted up the kerb.
Both drawings give the same answer to the weight of the wheel since it is done by taking the torque relative to the point of contact.
Attachments
Last edited: