phase0
- 6
- 1
Summary:: I am not sure about how can I write an appropriate equation to a question which include friction force and initial velocity.
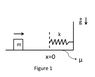
I came across a question that I am not sure how to write an equation.In the question, there is an object of mass m that is thrown into spring at v initial velocity.As soon as the spring starts to compress, the friction force also starts to act and we know the friction coefficient and spring constant.So in this case, how can we find the initial velocity and the final velocity in equilibrium state? I have foun an equation but I am not sure about how can I do it in latex ##m\dfrac{d^{2}x}{dt^{2}}+c\dfrac{dx}{dt}+kx=F_{0}\cos Wt## if you have any idea please share with me
[Moderator's note: moved from a technical forum.]
I came across a question that I am not sure how to write an equation.In the question, there is an object of mass m that is thrown into spring at v initial velocity.As soon as the spring starts to compress, the friction force also starts to act and we know the friction coefficient and spring constant.So in this case, how can we find the initial velocity and the final velocity in equilibrium state? I have foun an equation but I am not sure about how can I do it in latex ##m\dfrac{d^{2}x}{dt^{2}}+c\dfrac{dx}{dt}+kx=F_{0}\cos Wt## if you have any idea please share with me
[Moderator's note: moved from a technical forum.]
Last edited by a moderator: