Hooke's Law Lab Spring Constant Calculation

[Abhishekkkk__]

Homework Statement

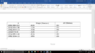
I need to calculate a spring constant using measurements from a Hooke's Law Apparatus, a spring, and some weights. The weights are hung vertically from the spring and the distance is measured from the equilibrium point of the spring. If I'm solving for k, then k=F/x. I do this for the different lengths of the spring and masses of the weights, and get very different answers for the constant. So here are my questions: 1) Am I even using the right formula? If I'm not, you can go give me the right one. 2) Shouldn't a constant be constant? And help on this matter would be greatly appreciated.

Homework Equations

The Attempt at a Solution

 

[Chestermiller]

Do you get a straight line if you plot weight versus Delta x?

 

[Abhishekkkk__]

Do you get a straight line if you plot weight versus Delta x?

Yes I do

 

[Chestermiller]

So the spring constant is the slope, and maybe you were off a little on the inextended length.