How are expectation values calculated?

[Cosmossos]

Hello,
Can someone explain to me how the expectation values are calculated in the following picture:

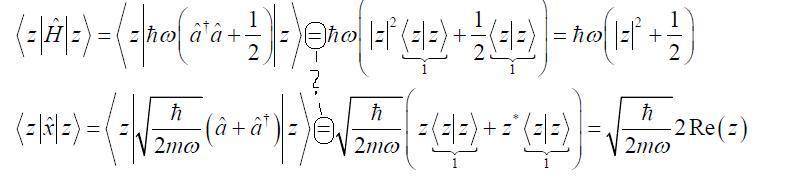
I mean , What did they do after the brackets? What did they multiply with what?
thanks

 

[Derivator]

what kind of states are those |z> states?

If those were enrgy-eigen-states of the harmonic oscillator, <z|a^\dagger a|z> \neq |z|^2.

<z|a^\dagger a|z> = z would be correct.

 

[Cosmossos]

Yes, I'm talking about harmonic oscillator. I don't understand how did they get the avg expression with the zs. (from the question mark to the right)

For exmple, what's the value of <z|a|z> , <z|a+|z> etc. and why?

 

[Derivator]

Yes, I'm talking about harmonic oscillator. I don't understand how did they get the avg expression with the zs. (from the question mark to the right)

For exmple, what's the value of <z|a|z> , <z|a+|z> etc. and why?

<z|a|z> =<z|a+|z>=0

since a and a+ are creation and annihilation operators:
a|z> is proportional to |z-1>
a+|z> is proportional to |z+1>

for further explanation please see this pdf file: http://iftia9.univ.gda.pl/~sjk/skok/ou01.pdf

 

[Cosmossos]

Thank but I don't see there how to calculate mean value (expectation value) of x and p for exmple. Can you try to explain to me how did they got what they wrote in the picture I attached earlier?

should I calculate them with integral accordering to the formula <a|x|a>=integral(a*xa)?
But it seems like they did it in a much simpler and easy way.

 

[Derivator]

You can write x and p in terms of a and a+

since by definition:

a := \sqrt{\frac{m\omega}{2\hbar}}(x+\frac{ip}{m\omega})
and
a^\dagger := \sqrt{\frac{m\omega}{2\hbar}}(x-\frac{ip}{m\omega})

You can invert these two formulas to get x an p:

x = \sqrt{\frac{\hbar}{2m\omega}}(a+a^\dagger)
p = \sqrt{\frac{\hbar m \omega}{2}}i(a^\dagger-a)

Now you can use formulas 8.38a and 8.38b from the pdf-file to calculate x and p.

 

[Cosmossos]

o.k I'll try it, and is true :

 

[Derivator]

o.k I'll try it, and is true :
View attachment 22838

please give some context