I How can a process be isentropic but not reversible or adiobatic?

[bardia sepehrnia]

TL;DR

Thermodynamics, entropy and reversibility

In the book for our thermodynamics, it states that a process that is internally reversible and adiabatic, has to be isentropic, but an isentropic process doesn't have to be reversible and adiabatic. I don't really understand this. I always thought isentropic and reversible mean the same thing, process that leads to no entropy generation should be by definition, reversible?
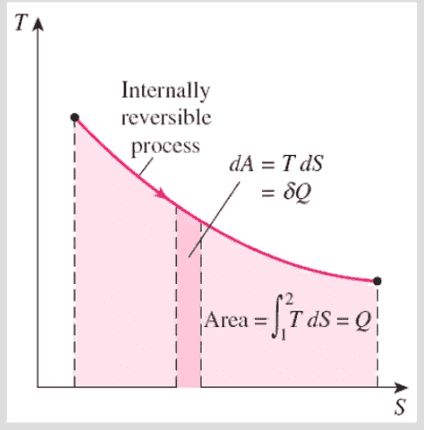
The book also keeps mentioning the word "internally" reversible which I don't understand what it means despite reading about it from 100 different sources.

So can anyone give me an example of:
1- An isentropic process that is not reversible not adiabatic? (no entropy generated, yet heat is transferred?)
2- A reversible process that is "not" adiabatic and "not" isentropic? (A graph in the book demonstrate that a process can be reversible, despite heat transfer)

 

[Chestermiller]

Let's first talk about an "internally reversible" process. An internally reversible process is one in which the system passes through a continuous sequence of thermodynamic equilibrium states. This does not say anything about what is happening in the surroundings (which may contain irreversibilities). An example of such a situation is one in which the system is gas in a cylinder with a piston that is allowed to expand isothermally and reversibly. The surroundings may consist of a constant temperature reservoir at a higher temperature than the system, with an intervening low thermal conductivity "insulation" through which the heat flows. The gas experiences a reversible expansion, but the surroundings experience an irreversible change because of the entropy generated within the intervening insulating layer. But, for the system, the process is internally reversible. However, overall, the combination of system plus surroundings experiences an increase in entropy.

An example of an isentropic process that is not reversible nor adiabatic is one in which an engine is working in a cycle, and the working fluid is undergoing an irreversible cycle. In this case, since the working fluid returns to its original state after each cycle, the process is isentropic with respect to the system (the working fluid). This doesn't say anything about the entropy change of the surroundings, which may consist of constant temperature reservoirs.

An example of a reversible process that is not adiabatic and not isentropic is the reversible isothermal expansion of a gas. This process is internally reversible with respect to the gas, even though its entropy increases.

So, in summary, some of the problem you are experiencing may be the result of confusing the entropy change of a system with the entropy change for the combination of system plus surrounding. The former can be positive, negative, or zero, depending on the nature of the process, but the latter can only be positive (irreversible process) or zero (reversible process).

 

[bardia sepehrnia]

Thank you