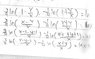How can I convert this function into a differential equation?

[hotjohn]

Homework Statement

dy/dx = (2x +y -1) / ( 4x -2y +1) , x= X +1 , y = Y-1 ,, how to make it into differential equation ? my ans is not same as the ans given .
P/s : in the second photo , it's lnx +c , sorry for the blur photo

Homework Equations

The Attempt at a Solution

 

[HallsofIvy]

What you give already is a differential equation! Do you mean "change from a differential equation in x and y to a differential equation in X and Y"? If you can immediately replace x and y on the right side of the equation by X+ 1 and Y- 1. For the left side, use the "chain" rule:
\frac{dy}{dx}= \frac{dy}{dY}\frac{dY}{dx}= \frac{dy}{dY}\frac{dY}{dX}\frac{dX}{dx}.

 

[hotjohn]

What you give already is a differential equation! Do you mean "change from a differential equation in x and y to a differential equation in X and Y"? If you can immediately replace x and y on the right side of the equation by X+ 1 and Y- 1. For the left side, use the "chain" rule:
\frac{dy}{dx}= \frac{dy}{dY}\frac{dY}{dx}= \frac{dy}{dY}\frac{dY}{dX}\frac{dX}{dx}.

in the photo posted , i have already showed that dy/ dY = 1 , dx/dX =1 , so i can conclude that dy=dY , dx=dX , so for the original dy/dx , i can make it as dY/dX , and replace the x as X+1 , and y = Y+1 , so i have dY/dX = (2X+Y) / (X+2Y)

 

[hotjohn]

in the photo posted , i have already showed that dy/ dY = 1 , dx/dX =1 , so i can conclude that dy=dY , dx=dX , so for the original dy/dx , i can make it as dY/dX , and replace the x as X+1 , and y = Y+1 , so i have dY/dX = (2X+Y) / (X+2Y)

But , i still didnt get the ans

 

[HallsofIvy]

Well, what was the "ans given"? And are you sure you are not getting it? In your first post, you have your answer as an equation involving several logarithms. You can use the "laws of logarithms" to reduce your equation to "ln(A)= ln(B)" and then take the exponential of both sides to get "A= B".