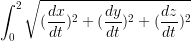How can I write complex equations using Reverse Polish notation?

[Synetos]

So I need some help with RPN, I checked the wiki page but I still don't quite get it. Like I get simple multiplications, aditions etc. But how would you for example write:

 

[Mark44]

So I need some help with RPN, I checked the wiki page but I still don't quite get it. Like I get simple multiplications, aditions etc. But how would you for example write:

Let me simplify things a bit, using x', y', and z' for values the derivatives, so that x' means the value of dx/dt at some specific t. Same for y' and z'.

To get the value of the radical you could do this:
x' Enter X² y' Enter X² + z' Enter X² + Sqrt

I'm thinking in terms of how you would evaluate a similar expression on an RPN calculator, such as the HP 48.

In the expression above X² is the operation that pops the value at the top of the stack, squares it, and stores the squared value at the top of the stack.
Enter is the operation that stores the value preceding it on the stack.
+ is the operation that pops the top two values on the stack, adds them, and stores their sum at the top of the stack.
Sqrt pops the top of the stack, takes the square root of it, and stores that value on the stack top.

 

[Unrest]

So I need some help with RPN, I checked the wiki page but I still don't quite get it. Like I get simple multiplications, aditions etc. But how would you for example write:

It's the way you'd do it in your head if you didn't want to remember too many intermediate results. There are different things you might want to use as operators, I made it simple with d/dt and integrate. You might instead have a d?/d? operator which takes two parameters, the function and the variable to differentiate with respect to.

Find x
Apply d/dt to it
Square it
Find y
Apply d/dt to it
Square it
Add the results of those two squarings
Find z
Apply d/dt to it
Square it
Add the result of the previous sum to this last result
Square root it
Integrate it

Rewritten in one line it becomes
x d/dt ² y d/dt ² + z d/dt ² + SqRoot Integrate

To interpret that it might be clearer with brackets. Each operator applies to the "thing" immediately before it. Or two things in case of the + operator.
( < [ ((x d/dt)²) ((y d/dt)²) + ] [ (z d/dt)² ] + >SqRoot )Integrate