How did the teacher get the third zero?

[supernova1203]

I understand how he got -120 and 360 as zeros, but then there is another zero 240, how did he get that?

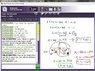
Check the diagram i have posted (which was done by the teacher) for simpler version

A bit of background:

we are working with sine functions the equation being
y=2sin(x-30)+1

so we re arrange y=sin(x-30)=-1/2

using special triangles/angles learned in previous lessons i deduce that since we are working with with sin and special angle 30, the ratio is 1/2 but since it is negative i also deduce that using the CAST rule (AllA positive in quadrent I ,only sinS positive in quadrent II,
only tan T positive in quadrent III, and only cosC positive in Quadrent IV
hence CAST) that the triangle ( or terminal arms) are in Q III and Q IV

according to the rules i learned here on these very forums

If theta is in QII then 180-theta
If theta is in QIII then theta -180
If theta is in QIV then 360-theta
There is no referrence angle in QI because in QI the main angle is the same thing as the referrence angle

using those rules i find QIII = theta - 180
30-180 = -150

then sub it back into the original equation sin(x-30)=-1/2
x-30=-150
x=-150+30
x=-120
One of the zeros is -120
similarly

QIV = 360-theta
360-30
=330
sub into original equation
sin(x-30)=-1/2
x-30=330
x=330+30
x=360
One of the zeros is 360...

the teacher somehow finds another zero which is 240...i have no idea how.Ok i see how he did it, but it makes no sense when i try to use the rules
"If theta is in QII then 180-theta
If theta is in QIII then theta -180
If theta is in QIV then 360-theta
There is no referrence angle in QI because in QI the main angle is the same thing as the referrence angle"
because he is doing it visually, and I am doing it the non visual way

 

[eumyang]

If theta is in QII then 180-theta
If theta is in QIII then theta -180
If theta is in QIV then 360-theta
There is no referrence angle in QI because in QI the main angle is the same thing as the referrence angle

using those rules i find QIII = theta - 180
30-180 = -150

You're mixing up here. θ is not the reference angle. They are angles in the different quadrants. What you wrote shows how to get the reference angle from θ. So, if you want to find an angle in Q III with reference angle 30°, you do this:

θ - 180° = 30°
or θ = 210°.
But θ is the angle whose sine is -1/2, or θ = x - 30°. So x = 240°.

In Q IV, you set up like this:
360° - θ = 30°
or θ = 330°.
Again, since θ = x - 30°, x = 360°.

Those are the only two angles you need. You also had x = -120°, but because θ = x - 30°, θ = -150°. -150° is coterminal with 210°, so there really is no need to list the answer x = -120°, unless x is restricted in some way.

For instance, in many problems like this, the directions would include 0° ≤ x < 360° as the restriction for x. If that is the case for your problem, then you would have to say that the answers are x = 0° and x = 240°. You would have to change the answer x = 360° to x = 0°, because x has to be less than 360°, so you have to get the coterminal angle for 360° within the range of x.

 

[supernova1203]

You're mixing up here. θ is not the reference angle. They are angles in the different quadrants, what you wrote shows how to get the reference angle from θ. So, if you want to find an angle in Q III with reference angle 30°, you do this:

θ - 180° = 30°
or θ = 210°.

ohh so if the referrence angle is not known you use those rules but if it is known you do
θ - 180° = 30°?
so those rules are for finding reference angles but if we have the reference angles then we do that θ - 180° = 30°?

 

[eumyang]

ohh so if the referrence angle is not known you use those rules but if it is known you do
θ - 180° = 30°?
so those rules are for finding reference angles but if we have the reference angles then we do that θ - 180° = 30°?

I really don't think of these as rules -- there are plenty of "rules" in trig as it is. But if you want a summary, I guess you could write them this way:

If φ is the reference angle and you want to find the corresponding angle θ in the different quadrants,
In Q I, θ = φ
In Q II, θ = 180° - φ
In Q III, θ = φ + 180°
In Q IV, θ = 360° - φ