aleksbooker
- 22
- 0
How did they "divide the equations"?
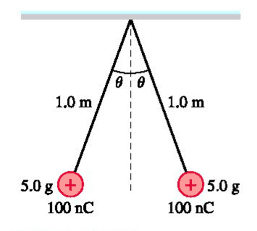
Two 5.0g point charges on 1.0m-long threads repel each other after being charged to +100nC.
What is angle theta? You can assume theta is a small angle.
K=9.0*10^9 Nm^2/C^2
g=9.8m/s^2
q=\frac{K|q_1||q_2|}{d^2}
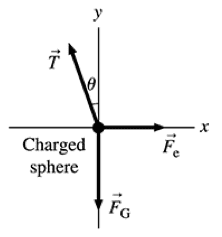
I determined my unknowns and translated everything into standard units, and drew out the free-body diagram.
Translated everything into standard units.
5.0g = 5.0*10^(-3) kg
100nc = 100*10^(-9) C
\frac{1}{2}d=\sin{\theta}
d=2\sin{\theta}
T_x=T\sin{\theta}=F_{2on1}=\frac{Kq^2}{d^2}
T_x=T\sin{\theta}=F_{2on1}=\frac{Kq^2}{(2\sin{\theta})^2}
T_x=T\sin{\theta}=F_{2on1}=\frac{Kq^2}{4sin^2{\theta} }
T_y=T\cos{\theta}=mg
The "missing" step:
The solutions manual says that the next step from here is to "divide the two equations and solve for q". What I don't know is how they "divided the two equations" to get this:
\sin^2{\theta}\tan{\theta}=\frac{Kq^2}{4L^2mg}=4.59*10^{-4}
Homework Statement
Two 5.0g point charges on 1.0m-long threads repel each other after being charged to +100nC.
What is angle theta? You can assume theta is a small angle.
Homework Equations
K=9.0*10^9 Nm^2/C^2
g=9.8m/s^2
q=\frac{K|q_1||q_2|}{d^2}
The Attempt at a Solution
I determined my unknowns and translated everything into standard units, and drew out the free-body diagram.
Translated everything into standard units.
5.0g = 5.0*10^(-3) kg
100nc = 100*10^(-9) C
\frac{1}{2}d=\sin{\theta}
d=2\sin{\theta}
T_x=T\sin{\theta}=F_{2on1}=\frac{Kq^2}{d^2}
T_x=T\sin{\theta}=F_{2on1}=\frac{Kq^2}{(2\sin{\theta})^2}
T_x=T\sin{\theta}=F_{2on1}=\frac{Kq^2}{4sin^2{\theta} }
T_y=T\cos{\theta}=mg
The "missing" step:
The solutions manual says that the next step from here is to "divide the two equations and solve for q". What I don't know is how they "divided the two equations" to get this:
\sin^2{\theta}\tan{\theta}=\frac{Kq^2}{4L^2mg}=4.59*10^{-4}