How Do Bead Speeds Relate on a Semicircular Wire with a Tight String?

[Saitama]

Homework Statement

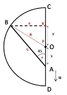
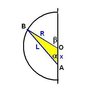
Two beads A and B move along a semicircular wire frame as shown in the figure as shown in figure. The beads are connected by an inelastic string which always remains tight. At an instant the speed of A is u, angle BAC is 45 degrees and angle BOC is 75 degrees, where O is the centre of semicircular arc. The speed of bead B at that instant is.

Homework Equations

The Attempt at a Solution

I really have no idea on how to begin with this. How should i go on forming equations?
Please point me in the right direction.

Thanks!

 

[Infinitum]

Hi again

Since the string is not extensible, the vertical velocity of B will always have to be equal to the velocity of A. Can you frame an equation for this?

 

[Saitama]

Hi again

Since the string is not extensible, the vertical velocity of B will always have to be equal to the velocity of A. Can you frame an equation for this?

I did that once but i thought i am trying my own foolish things.
I assumed that at any instant the distance of A from O is x and that of B is y.
l=(x+y)cos45
Differentiating with respect to time, i get:
(dy/dt)=-(dx/dt)

How can i proceed further?

 

[Infinitum]

l=(x+y)cos45

Umm noo..how did you get that?

You can simply equate the vertical velocity component of B to u. The velocity of B will be have its direction tangential to the ring...what does this tell you about its vertical component?

 

[TSny]

Hi again

Since the string is not extensible, the vertical velocity of B will always have to be equal to the velocity of A. Can you frame an equation for this?

Hello, Infinitum. I don't see how your statement can be true. If the vertical component of velocity of B equals the velocity of A, then during a time Δt, both particles would move the same distance vertically. But B will also move horizontally during this time. So, it seems to me that this would change the distance between A and B.

 

[TSny]

Homework Equations

The Attempt at a Solution

I really have no idea on how to begin with this. How should i go on forming equations?
Please point me in the right direction.

You might give us some context for the problem since there are different methods for solving it. If it's a "related rates problem" from a calculus course then you would be expected to use calculus. Or if it's a problem where you can use any method you want, then you can solve it with just geometry, trig, and some insight.

 

[Saitama]

Umm noo..how did you get that?

You can simply equate the vertical velocity component of B to u. The velocity of B will be have its direction tangential to the ring...what does this tell you about its vertical component?

Sorry, i think i did not explain it correctly. My assumption can be better shown by this pic:

So what i did was incorrect? and why?

You might give us some context for the problem since there are different methods for solving it. If it's a "related rates problem" from a calculus course then you would be expected to use calculus. Or if it's a problem where you can use any method you want, then you can solve it with just geometry, trig, and some insight.

Well, it isn't specified that i need to do the problem by a specified method, any method will do.

...you can solve it with just geometry, trig, and some insight.

Would you be so kind to tell me how i can solve by this?

 

[ehild]

Hi Pranav,

The angles change with time so just call them α and β or anything else. Find relation between them and x. You know that u=dx/dt. The speed of the other bead on the circle is v=R|dβ/dt|. You need to differentiate, using that the length of the cord is constant in time, and so is the radius of the circle.

ehild

 

[Saitama]

Hi Pranav,

The angles change with time so just call them α and β or anything else. Find relation between them and x. You know that u=dx/dt. The speed of the other bead on the circle is v=R|dβ/dt|. You need to differentiate, using that the length of the cord is constant in time, and so is the radius of the circle.

ehild

Hello ehild!

As you said i tried finding some relations,
Ist relation, Lsin(α)=Rsin(β)=d
IInd Relation, Lcos(α)-Rcos(β)=x
Differentiating the second relation with respect to time,

Rsin(β)(dβ/dt)-Lsin(α)(dα/dt)=dx/dt
I can use the first relation here but i don't seem to reach the answer.

 

[azizlwl]

Instead of using law of sines, why not try using law of cosines.

 

[Infinitum]

Hello, Infinitum. I don't see how your statement can be true. If the vertical component of velocity of B equals the velocity of A, then during a time Δt, both particles would move the same distance vertically. But B will also move horizontally during this time. So, it seems to me that this would change the distance between A and B.

Hi TSny. You are right, I meant to write that the velocity component of A along the length of the rod has to be equal to the velocity component of B along the length of the rod, so that the rod length remains the same.

 

[Infinitum]

Sorry, i think i did not explain it correctly. My assumption can be better shown by this pic:

So what i did was incorrect? and why?

Oh, I see. You had mentioned that the distance of B from O is y earlier, that led me into confusion

I also made a little mistake while saying their vertical components are equal. Instead, their velocities along the rod have to be the same, for no extension.

 

[Saitama]

Oh, I see. You had mentioned that the distance of B from O is y earlier, that led me into confusion

I also made a little mistake while saying their vertical components are equal. Instead, their velocities along the rod have to be the same, for no extension.

Umm..so what i did is incorrect?

How should i proceed now?

 

[Infinitum]

Umm..so what i did is incorrect?

Yes, you got "l=(x+y)cos45"

But it should be $lcos45 = x+y$

And you cannot simply differentiate this because the angle is changing continuously, as ehild indicated.

How should i proceed now?

An easier approach is equating the velocities of A and B along the rod. Let the velocity of B be v, and then try to solve the problem.

 

[Saitama]

An easier approach is equating the velocities of A and B along the rod. Let the velocity of B be v, and then try to solve the problem.

Oh, that's a nice hint, thanks for the help, i got the answer.

 

[Infinitum]

Oh, that's a nice hint, thanks for the help, i got the answer.

Way to go!

 

[TSny]

Hi TSny. You are right, I meant to write that the velocity component of A along the length of the rod has to be equal to the velocity component of B along the length of the rod, so that the rod length remains the same.

That's a very nice way to solve it.

I had solved it by setting up a velocity triangle based on

V_B = V_A + V_B/A . (vector addition!)

where V_B/A is the velcity of B relative to A. V_B/A must be perpendicular to line AB in order for AB to keep a fixed distance apart. This is similar to your statement that the velocity components of A and B along line AB must be equal. From the velocity triangle you can then use the law of sines to get the result.

But I like your approach much better. It gets the answer right away.

Thanks.

 

[ehild]

An easier approach is equating the velocities of A and B along the rod. Let the velocity of B be v, and then try to solve the problem.

It is ingenious, Infinitum!

My method is much more complicated.
The speed of the bead on the vertical line is dx/dt=u.
The speed of the bead on the circle is v=Rdβ/dt=Rω

From the cosine law in the tringle AOB,

$$L^2=R^2+x^2+2Rxcos(\beta)$$

With implicit differentiation,

$$0=x u+R u cos(\beta)-Rx\sin(\beta) ω$$

isolating v=Rω

$$v=u\frac{(1+\frac{R}{x}cos(\beta))}{\sin(\beta)}$$

Form the sine law, $$\frac{R}{x}=\frac{\sin(\alpha)}{\sin(\beta-\alpha)}$$

Plugging in and simplifying, we get:

$$v=u\frac{cos(\alpha)}{\sin(\beta-\alpha)}$$

ehild

 

[Saitama]

The speed of the bead on the vertical line is dx/dt=u.
The speed of the bead on the circle is v=Rdβ/dt=Rω

From the cosine law in the tringle AOB,

$$L^2=R^2+x^2+2Rxcos(\beta)$$

With implicit differentiation,

$$0=x u+R u cos(\beta)-Rx\sin(\beta) ω$$

isolating v=Rω

$$v=u\frac{(1+\frac{R}{x}cos(\beta))}{\sin(\beta)}$$

Form the sine law, $$\frac{R}{x}=\frac{\sin(\alpha)}{\sin(\beta-\alpha)}$$

Plugging in and simplifying, we get:

$$v=u\frac{cos(\alpha)}{\sin(\beta-\alpha)}$$

ehild

It's really complicated.
Thanks for an alternative solution.