sterlingm
- 2
- 0
Hi,
I want to find the world coordinates of the center of a square given:
-The top left corner is the reference point
-Its position relative to the world frame
-Its orientation relative to the world frame
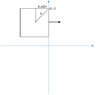
The example that I have been using is that the square is at (0,2), has 0 orientation, and the distance to the center from the corner is 0.1524m in the x and y directions (Picture given).
View attachment 1868
This means that the center should be -0.1524, 1.8476. My closest way of doing it was:
x = x_world + (h*cos(-PI/4))
y = y_world + (h*sin(-PI/4))
h = 0.2155m for this example
However, this gives me the location of (0.1524, 1.8476). The x coordinate should be negative. I have tried numerous equations such as:
x = (x_world+h)*(cos(orientation - PI/4))
x = (x_world+h)*(cos(orientation + PI/4))
x = x_world*cos(orientation+PI/4)
(The y formulas being the same but replacing x with y and cos with sin)
However, none of these work. If anyone could help me out, that would be great. I feel like it should be so simple, but I can't seem to figure it out. The oddly specific example is not from homework, this is something I am working on for a hobbyist 2D project.
I want to find the world coordinates of the center of a square given:
-The top left corner is the reference point
-Its position relative to the world frame
-Its orientation relative to the world frame
The example that I have been using is that the square is at (0,2), has 0 orientation, and the distance to the center from the corner is 0.1524m in the x and y directions (Picture given).
View attachment 1868
This means that the center should be -0.1524, 1.8476. My closest way of doing it was:
x = x_world + (h*cos(-PI/4))
y = y_world + (h*sin(-PI/4))
h = 0.2155m for this example
However, this gives me the location of (0.1524, 1.8476). The x coordinate should be negative. I have tried numerous equations such as:
x = (x_world+h)*(cos(orientation - PI/4))
x = (x_world+h)*(cos(orientation + PI/4))
x = x_world*cos(orientation+PI/4)
(The y formulas being the same but replacing x with y and cos with sin)
However, none of these work. If anyone could help me out, that would be great. I feel like it should be so simple, but I can't seem to figure it out. The oddly specific example is not from homework, this is something I am working on for a hobbyist 2D project.