NWNINA
- 7
- 0
Homework Statement
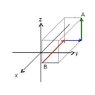
Calculate V(ab) if E = (-5 y / x^3) ax + (5/x) ay + 4 az V/m.
A(-8,3,2) and B(5,2,3).
Homework Equations
Vab=-∫Edl
The Attempt at a Solution
So I tried
V=-[∫(-5y/x^3)dx {from 5 to -8}+ ∫(5x)dy {from 2 to 3} + ∫4dz {from 3 to 2}]
The problem is that the limits are wrong. What should I do?
Should it be the distance and not the literal point on the plane? like the first one, should it be 0 to 13, the second one 0 to 1, the third one 0 to 1?
and what do I do with the remaining variables after the integration. For ex, in the first one I would have a y and on the second one a x