How do I determine the resistance for RLC low pass filter?

[rickyw2777]

Homework Statement

A music filter. Cheap or low-quality audio amplifiers can add noise to an audio recording that is
distracting and undesired. Two examples are a white-noise “hiss” across all frequencies, which
arises from electrons that randomly move inresponse to thermal fluctuations, and a 60Hz “hum”,
which comes from the electrical grid itself (power lines and electrical wires within buildings)
coupling inductively into the circuit.

Our objective is to design an RLC filter to remove these noise sources while allowing the audio
itself (e.g., tones from musical instruments and speech) to get through. The time-series vector 𝑣in
will represent the noisy music, which could be carried on an audio cable from a phone, laptop, or
stereo system, and 𝑣out represents the filtered audio signal from your circuit.

Relevant Equations

V_{in}-V_L-V_c-V_R=0;
V_{c,k+1} = V_{c,k} +(h/c)*i_k;
V_{R,k} = i_k*R;
i_{k+1} = i_k +(h/L)*V_{L,K};

Hi, I am trying to build a RLC low pass filter that atenuates the frequency below 4500 Hz. However, I have encountered some problem when choosing the correct R to work with.
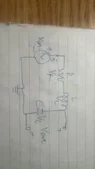
Here is the Circuit

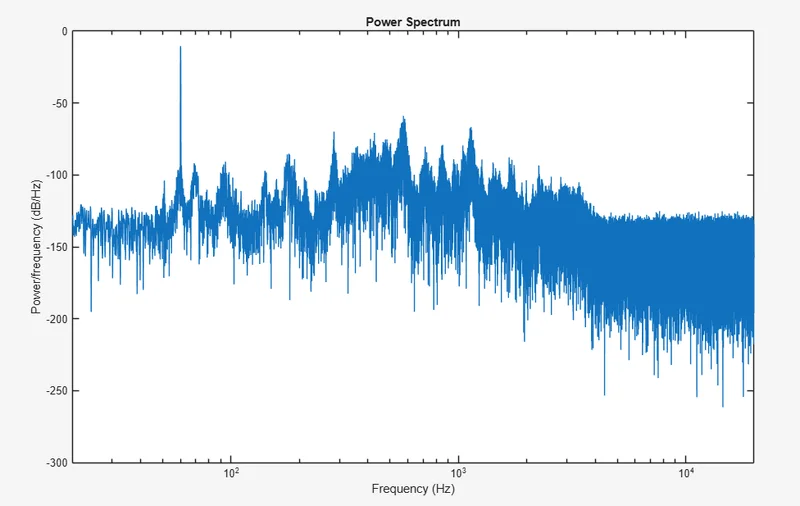
Here is the original sound.

Here is my code in Matlab

function Vout = myFilterCircuit(Vin,h)
n_V = length(Vin);
f_7 = 4470;; % Undesired frequency
h_7 = h; % delta time
% These are for the constant and initialization of the variables
t_7 = 0:h_7:(n_V-1)*h_7; % This is the independent variable

LC_2 = 1/((f_7*2*pi)^2);% This is for L C
R_7 = 0.0001; % This is R
L_7 = 1*10^-3; % This is L
C_7 = LC_2/L_7; % This is C
%
A_2 = [1,h_7/C_7;-h_7/L_7,1-h_7*R_7/L_7]; % This is the A matrix
B_2 = [0;h_7/L_7]; % This is the B matrix
C_2 = [1,0]; % This is the C matrix
D_2 = [0]; % This is the D matrix
%
sys_8 = ss(A_2,B_2,C_2,D_2,h_6); % This is the system
[y_8,tout_8,x_8] = lsim(sys_8, V_inter, t_7); % Simulate the system response
%
Vout = y_8(:,1); % This is the V_c output.

figure;
bode(sys_7, sys_8);
legend('60Hz LPF', '4470Hz LPF');

end

Here is the Bode Diagram

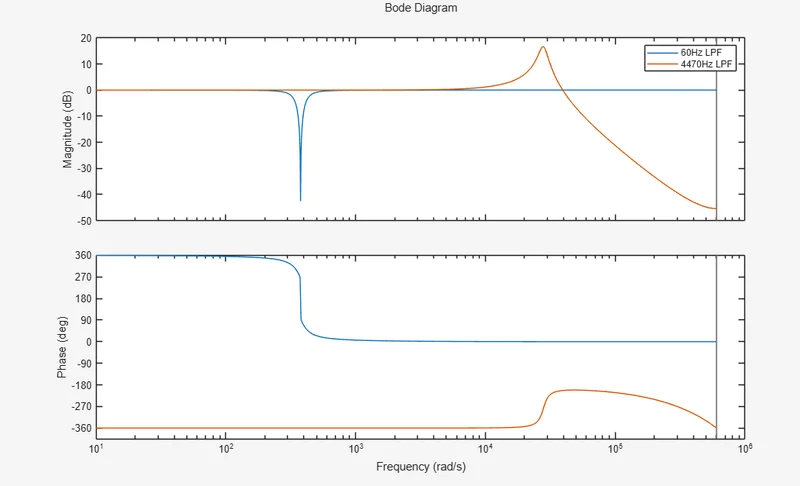
So you can see I used the inductance of 1*10^-3, and capacitance around 1.26*10^-6. I try to use the resistance of 0.0001, but it does not work. And the system of equation eventually becomes not solvable. Please let me know what value of R I should choose.

 

[BvU]

Hi,

Interesting exercise. Your post is rather incomplete though, and also hard to follow.
Cosmetically: you want to enclose code with the tags [code=matlab] ... [/code]

function Vout = myFilterCircuit(Vin,h)
n_V = length(Vin);
f_7 = 4470;; % Undesired frequency
h_7 = h; % delta time
% These are for the constant and initialization of the variables
t_7 = 0:h_7:(n_V-1)*h_7; % This is the independent variable
%etc

I only have Octave instead of matlab, but it tells me I need to run pkg load control to use the ss function.

Furthermore, your code only shows a function, not what is calling the function. So Vin and h are unknown; further down h_6 is unknown and so is V_inter.

I personally have no idea what matrices A, B, C, D represent, but that may be just ignorance.

build a RLC low pass filter that atenuates the frequency below 4500 Hz

Do you mean "attenuates frequencies above 4500 Hz" ? What about the 60 Hz ?

R = 0.0001 is unrealistically low.

Can you explain what the variables in your relevant equations are ?

$\$

 

[rickyw2777]

My bad, it should be keep the frequency lower than 4500 Hz and Atenuates the frequency above 4500 Hz.

The 60 Hz should be reduced by a RLC bandpass filter.

A, B, C D are just the matrix representation of the set of differential equations.

you can see my note here

I guess just generally what is the factor that determines how quickly the amplitude decays for the low pass filter.