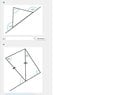
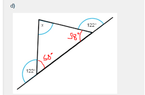
For the first question, you need to know two things.
1. A straight lines forms an angle of 180 degrees
2. All angles in a triangle must add up to 180 degrees.
Use the first principle to solve for the two interior angles of the triangle other than x. It would look like this:
180 degrees = 122 degrees + interior angle
interior angle = 180 degrees - 122 degrees = 58 degrees.
The calculation is the same for both angles, since they are both 122 degrees.
View attachment 9131
Now you have a triangle with interior angles 58 degrees, 58 degrees, and x.
Use the second principle (all angles in a triangle add up to 180) to solve for x.
x + 58 degrees + 58 degrees = 180 degrees
x = 180 - 58 degrees - 58 degrees
x= 64 degrees.
For the second question, you need to know the two things above, plus the fact that
3. Isosceles triangles have two sides that are the same length, and therefore two angles that are the same measure. Those angles are the base angles.
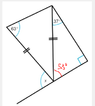
Start by looking at the triangle furthest to the right. You are given that the triangle has one right angle, and one angle that is 37 degrees. Using the fact that all angles add up to 180 degrees, solve for the third angle.
Third angle + 37 degrees + 90 degrees = 180 degrees
Third angle = 180 degrees - 37 degrees - 90 degrees.
Third angle = 53 degrees.
View attachment 9128
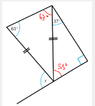
Now, move on to the second triangle. Use the fact that this triangle is isosceles, and therefor its base angles are the same. This means that the other base angle also has a measure of 63 degrees.
View attachment 9129
Now, we know two angles of the second triangle, and can solve for the third using the same method as above.
Third angle + 63 degrees + 63 degrees = 180 degrees.
Third angle = 180 degrees - 63 degrees - 63 degrees
Third angle = 54 degrees
View attachment 9130
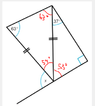
Now you can use the fact that a straight line forms an angle of 180 degrees to solve for x.
x + 54 degrees + 53 degrees = 180 degrees
x = 180 degrees - 54 degrees - 53 degrees
x = 73 degrees