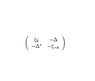aaaa202
- 1,144
- 2
For the attached matrix A I can find the eigenvalues:
λ\pm = \pm√(\xik2-lΔl2)
But when I try to solve for the eigenvectors I get it wrong:
I solve:
(A-λ\pm)(x,y) = (0,0)
gives the eigenvectors:
e\pm=(Δ,\xik\pm√(\xik2-lΔl2))
But these eigenvectors are not orthogonal. How do I get a complex conjugation of one of the deltas?
λ\pm = \pm√(\xik2-lΔl2)
But when I try to solve for the eigenvectors I get it wrong:
I solve:
(A-λ\pm)(x,y) = (0,0)
gives the eigenvectors:
e\pm=(Δ,\xik\pm√(\xik2-lΔl2))
But these eigenvectors are not orthogonal. How do I get a complex conjugation of one of the deltas?