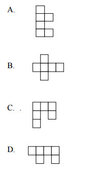
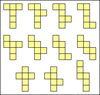
How Do I Identify the Net of a Cube?

  • Context: MHB 
  • Thread starter Thread starter susanto3311
  • Start date Start date
  • Tags Tags
    Cube Net
Click For Summary
SUMMARY

Identifying the net of a cube involves recognizing the arrangement of its six square faces. A valid net can be formed if one square has three adjacent squares or if two squares each have two adjacent squares. This method simplifies the process of visualizing and constructing the net of a cube, making it easier to understand the spatial relationships between the faces.

PREREQUISITES
  • Understanding of geometric shapes, specifically cubes
  • Familiarity with the concept of adjacent faces in three-dimensional objects
  • Basic knowledge of spatial visualization techniques
  • Experience with drawing or modeling geometric nets
NEXT STEPS
  • Research geometric nets and their properties
  • Explore visual aids for constructing nets of three-dimensional shapes
  • Practice identifying nets for other polyhedra, such as pyramids and prisms
  • Learn about software tools for modeling geometric shapes, such as GeoGebra
USEFUL FOR

Students learning geometry, educators teaching spatial reasoning, and anyone interested in understanding the properties of three-dimensional shapes.

susanto3311
Messages
73
Reaction score
0
hello everybody...

i have problem, how to easy find & identify a net of the cube..

do you have a easy tricks/method to figure it out this problem?

thanks..
 

Attachments

  • nets problem.jpg
    nets problem.jpg
    4 KB · Views: 117
Mathematics news on Phys.org
susanto3311 said:
hello everybody...

i have problem, how to easy find & identify a net of the cube..

do you have a easy tricks/method to figure it out this problem?

thanks..

To identify the net of a cube, you must observe 6 squares (since a cube has 6 sides).
Either one square should have 3 adjacent squares, or 2 squares should have 2 adjacent squares, or both.

Follow the same procedure to find the net of a cube. Like This :

 

Attachments

  • 11nets_cube.gif
    11nets_cube.gif
    2.4 KB · Views: 106
phymat said:
To identify the net of a cube, you must observe 6 squares (since a cube has 6 sides).
Either one square should have 3 adjacent squares, or 2 squares should have 2 adjacent squares, or both.

Follow the same procedure to find the net of a cube. Like This :

​

hi phymat...

it's great, very educational..

thanks.
 

Similar threads

High School Cube Math: How Many Smaller Cubes in a Larger Cube?
  • · Replies 4 ·
Replies
4
Views
4K
MHB How to Find the Cube Root of a Number?
  • · Replies 1 ·
Replies
1
Views
2K
Struggling to understand the concept of this question (ice cube in water optics question)
  • · Replies 29 ·
Replies
29
Views
1K
Insights Fermat's Last Theorem
  • · Replies 105 ·
4
Replies
105
Views
9K
Tungsten Cubes for STEM Education — Looking for Feedback
  • · Replies 2 ·
Replies
2
Views
500
High School Volume of a Cube: Definition & Explanation
  • · Replies 7 ·
Replies
7
Views
5K
Undergrad What do you call a parallelepiped that isn't a cube?
  • · Replies 3 ·
Replies
3
Views
1K
High School Self-descriptive Physical Object
  • · Replies 33 ·
2
Replies
33
Views
3K
Net charge contained by a cube in a region with a non-uniform E field
  • · Replies 3 ·
Replies
3
Views
3K
MHB How can I accurately create a 3D figure using given nets?
  • · Replies 3 ·
Replies
3
Views
1K