danik_ejik
- 18
- 0
Hello,
I need to simplify and find Re and I am of
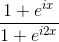 .
.
I've multiplied by
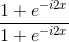 and got that Re=
and got that Re=
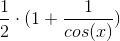 and Im=
and Im=
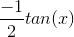 .
.
Is that the correct way and a correct result ?
I need to simplify and find Re and I am of
I've multiplied by
Is that the correct way and a correct result ?