MHB How Do I Solve This Garden Border Problem?

[Simonio]

Here's another question I'm finding it hard to get started on:

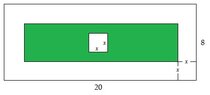
" A garden is in the shape of a rectangle, 20 metres by 8 metres. Around the outside is a border of uniform width, and in the middle is a square pond. The width of the border is the same as the width of the pond. The size of the are which is NOT occupied by either border or pond is \(124m^2\). Letting the width of the border be \(xm\), derive the equation \(3x^2-56x + 36 = 0\).

The only equation I can derive is this: A (total area) = \((2x + 20)(2x + 8)\). I'm not sure how to relate the information about the square and the inner area of \(124^2m\). Any help appreciated. I'm still finding these sort of questions difficult

 

[MarkFL]

First, let's draw a diagram:

View attachment 2584

Now, the area we want is shaded in green. The width of this area is $20-2x$ and the length is $8-2x$. Then we need to subtract the area of the pond, which is $x^2$. Can you put this all together and equate it to $124\text{ m}^2$ to obtain the required quadratic in $x$?

 

[Simonio]

First, let's draw a diagram:

View attachment 2584

Now, the area we want is shaded in green. The width of this area is $20-2x$ and the length is $8-2x$. Then we need to subtract the area of the pond, which is $x^2$. Can you put this all together and equate it to $124\text{ m}^2$ to obtain the required quadratic in $x$?

Thanks. Wow, I misread the meaning and thought that the 20x8 dimension was for the inner garden area -I find it's easy to get verbally confused! I'll have a go now based on your diagram -thanks a lot!

 

[Ackbach]

Ah, the importance of drawing a diagram cannot be overlooked. While a picture is never a proof, they can sure help to get the proof! (Or solution, in this case.)

Take a gander at the http://mathhelpboards.com/other-topics-22/problem-solving-strategy-28.html I've culled from various sources. It might help you out with word problems.

 

[DreamWeaver]

Ah, the importance of drawing a diagram cannot be overlooked. While a picture is never a proof, they can sure help to get the proof! (Or solution, in this case.)

Never a truer word said. [And for those who haven't already, and who might yet doubt the veracity of Ackbach's words, see Tristan Needham's "Visual Complex Analysis" (Heidy) ]