How Do Theta 1 and Theta 2 Relate in Different Right Triangles?

AI Thread Summary
The discussion centers on the relationship between the angles theta 1 and theta 2 in two right triangles with the same base but different heights. The first triangle has a height of h, while the second has a height of 2h. An algebraic proof is sought to establish the relationship, with a reference to the tangent function showing that tan(theta 1) equals twice tan(theta 2). However, it is clarified that theta 1 is not necessarily twice as large as theta 2, though this approximation holds true when the height h is significantly greater than the base a. The conversation emphasizes the need for a rigorous algebraic proof to fully understand the angle relationship.
Link
Messages
132
Reaction score
1
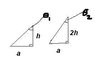
There are two right triangles, the first one with the base a and the height h. The second has the base a and 2h. The question is to prove the relationship between the theta 1 and theta 2 angles in the triangles (see attachment). I have been able to prove it with circle theorems but not with algebra, so i would appreciate if someone could deliver a algebraic proof, thank you.
 

Attachments

  • 1.JPG
    1.JPG
    3.8 KB · Views: 416
Mathematics news on Phys.org
Well, you should have:
tan(\theta_{1})=\frac{a}{h}=2\frac{a}{2h}=2tan(\theta_{2})
 
follow up

Does this mean theta 1 is twice as big as theta 2?
 
Link said:
Does this mean theta 1 is twice as big as theta 2?
In general, No. However, it is approximatly true when h>> a.
 

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »
Thread 'Imaginary Pythagorus'

Thread 'Imaginary Pythagorus'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

I Geometry problem of interest with a 3-4-5 triangle
2
Replies
59
Views
2K
B A Question Relating Sum of Angles and Breaking of the Parallel Postulate
Replies
6
Views
1K
I Determine ## \beta ## as a function of ##\theta## linkage
Replies
2
Views
2K
MHB Right Angled Triangle: Find $\sin(\theta)$
Replies
1
Views
1K
I Is e^pi a unique transcendental, or perhaps not transcendental?
Replies
1
Views
2K
MHB How do I get the book's answer for finding the area of a gable?
Replies
4
Views
1K
MHB Question about a rounded rectangle
Replies
1
Views
7K
B Proofs: Hypotenuse is the longest side of a right triangle
Replies
17
Views
10K
B How Can Trigonometry Calculate Distances in Surveying?
Replies
5
Views
2K
A Finding Minimal Mean Distance Curves on the Unit Sphere
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top