MHB How do we distribute the elements into schedules?

[mathmari]

Hey! :giggle:

The transactions $T_1, T_2,\ldots , T_7$, the database elements $A, B, C, D, E$ and the below multiset are given

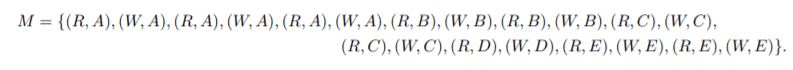
Now distribute the twenty elements from $M$ in three different ways so that three different schedules $S_1$, $S_2$ and $S_3$ arise. Also make sure that $S_1$ is a serial schedule, $S_2$ is a conflict serializable schedule, and $S_3$ is a non-conflict serializable schedule. Give the dependency graphs on S2 and S3.Do we distribute the elements of $M$ to the transactions $T_i$ arbitrarily ? :unsure:

 

[mathmari]

Can we first define arbitrarily the seven transactions and then define the three schedules so that $S_1$ is a serial schedult, $S_2$ is conflict serializableand $S_3$ is non-conflict serializable?

We have twenty elements and seven transactions, so should each transaction contain two elements and the six of the transactions have also a third element?

Do we define the transaction for example as follows ?
\begin{align*}&T_1 : ((R, A),(W, A)) \\ &T_2: ((R, A),(W, A)(R, A)) \\ &T_3 : ((W, A),(R, B),(W, B)) \\ &T_4 : ((R, B),(W, B),(R, C)) \\ &T_5: ((W, C), (R, C),(W, C)) \\ &T_6: ((R, D),(W, D),(R, E)) \\ &T_7 : ((W, E),(R, E),(W, E))\end{align*}
Is then a serial schedule \begin{align*}S_1&=((T_1, R, A),(T_1, W, A),(T_2, R, A),(T_2, W, A),(T_2, R, A),\\ & (T_3, W, A),(T_3, R, B),(T_3, W, B),(T_4, R, B),(T_4, W, B),(T_4, R, C),\\ & (T_5, W, C), (T_5, R, C),(T_5, W, C),(T_6, R, D),(T_6, W, D),(T_6, R, E),\\ & (T_7, W, E),(T_7, R, E),(T_7, W, E))\end{align*} ?

:unsure:

 

[I like Serena]

Hey mathmari!

After reading you notes in your other thread, I believe you are correct. (Nod)

 

[mathmari]

After reading you notes in your other thread, I believe you are correct. (Nod)

A schedule is called conflict serializable if it can be transformed into a serial schedule by swapping non-conflicting operations.

So we take $S_1$ and we swap at least two non-conflicting operations to get $S_2$. Is that correct?

So do we get the following ?
\begin{align*}S_2&=((T_7, W, E),(T_1, W, A),(T_2, R, A),(T_2, W, A),(T_2, R, A),\\ & (T_3, W, A),(T_3, R, B),(T_3, W, B),(T_4, R, B),(T_4, W, B),(T_4, R, C),\\ & (T_5, W, C), (T_5, R, C),(T_5, W, C),(T_6, R, D),(T_6, W, D),(T_6, R, E),\\ & (T_1, R, A) ,(T_7, R, E),(T_7, W, E))\end{align*} (I swapped the first element of the first line with the first element of the last line) Is that a conflict serializable schedule ? The result is not unique, is it? :unsure: For $S_3$ we have to consider a schedule at which even when we swap non-conflicting operations we don't get a serial schedule, right? :unsure:

 

[I like Serena]

I'm afraid that is not correct. (Shake)

In transaction $T_1$ we first read from A, and then we write to A.
When we put that read operation near the end, we will read what we (or some other transaction) wrote before, instead of what was there before we wrote.
In other words, the conflicting operations in the same transaction must remain in the same order.

I believe that we can also not put $(T_7, W, E)$ at the beginning, since then $T_7$ is not atomic any more. Other transactions will read the changed value in E while transaction $T_7$ has not been completed yet, and it will still read and write yet again to E.

Other than that, yes, we can just swap 2 operations, as long as we make sure that the transactions remain atomic and consistent.

 

[mathmari]

In transaction $T_1$ we first read from A, and then we write to A.
When we put that read operation near the end, we will read what we (or some other transaction) wrote before, instead of what was there before we wrote.
In other words, the conflicting operations in the same transaction must remain in the same order.

So when we move $(T_1, R,A)$ do we have to move also $(T_1, W, A)$ so that is again after $(T_1, R, A)$ ? :unsure:

I believe that we can also not put $(T_7, W, E)$ at the beginning, since then $T_7$ is not atomic any more. Other transactions will read the changed value in E while transaction $T_7$ has not been completed yet, and it will still read and write yet again to E.

What do you mean by atomic? I got stuck right now. :unsure:

 

[mathmari]

If we just swap $(T_5, W, C)$ and $(T_6, R, D)$, do we get a conflict serializable schedule or do we have to do more swaps ? \begin{align*}&((T_1, R, A),(T_1, W, A),(T_2, R, A),(T_2, W, A),(T_2, R, A),\\ & (T_3, W, A),(T_3, R, B),(T_3, W, B),(T_4, R, B),(T_4, W, B),(T_4, R, C),\\ & (T_5, W, C), (T_5, R, C),\textbf{(T_6, R, D)},\textbf{(T_5, W, C)},(T_6, R, D),(T_6, W, D),(T_6, R, E),\\ & (T_7, W, E),(T_7, R, E),(T_7, W, E))\end{align*}
:unsure:

 

[mathmari]

In general the transactions should always be in the form R-W or R-W-R-W ?

Then should the transactions be as follows ?
\begin{align*}&T_1 : ((R, A),(W, A), (R, A),(W, A)) \\ &T_2: ((R, A),(W, A)) \\ &T_3 : ((R, B),(W, B),(R, B),(W, B)) \\ &T_4 : ((R, C),(W, C)) \\ &T_5: ( (R, C),(W, C)) \\ &T_6: ((R, D),(W, D)) \\ &T_7 : ((R, E),(W, E),(R, E),(W, E))\end{align*}

:unsure:

 

[mathmari]

Then we have :
\begin{align*}S_1 : &((T_1,R, A),(T_1,W, A), (T_1,R, A),(T_1,W, A), \\ &(T_2,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_5,W, C), (T_6,R, D),(T_6,W, D), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*} We can swap $(T_5,W, C), (T_6,W, D)$ since they have different objects, so they are not in conflict.
\begin{align*} &((T_1,R, A),(T_1,W, A), (T_1,R, A),(T_1,W, A), \\ &(T_2,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_6,W, D), (T_6,R, D),(T_5,W, C), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*}
We can also swap $(T_1,R, A), (T_2,R, A)$ since they are both R, so they are not in conflict.
So we get:
\begin{align*}S_2 : &((T_1,R, A),(T_1,W, A), (T_2,R, A),(T_1,W, A), \\ &(T_1,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_6,W, D), (T_6,R, D),(T_5,W, C), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*} We can swap $(T_1,R, A),(T_1,W, A)$ since they are in conflict
\begin{align*} &((T_1,R, A),(T_1,W, A),(T_1,W, A), (T_1,R, A), \\ &(T_2,R, A),(T_2,W, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_5,W, C), (T_6,R, D),(T_6,W, D), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*}
We can swap also $(T_1,R, A),(T_2,W, A)$ since they are in conflict
\begin{align*}S_3 : &((T_1,R, A),(T_1,W, A),(T_1,W, A), (T_2,W, A), \\ &(T_2,R, A),(T_1,R, A), (T_3,R, B),(T_3,W, B),(T_3,R, B),(T_3,W, B), \\ &(T_4,R, C),(T_4,W, C), (T_5,R, C),(T_5,W, C), (T_6,R, D),(T_6,W, D), \\ &(T_7,R, E),(T_7,W, E),(T_7,R, E),(T_7,W, E))\end{align*} Are these schedules correct? :unsure: