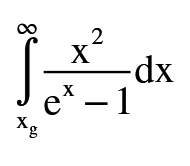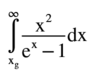I How do we integrate x^2/(e^x - 1) from xg to infinity?

[Max Loo Pin Mok]

How do we integrate this function? It is possible if the range is from 0 to infinity, but from x_g to infinity? This equation comes from page 512 of the 1961 paper by William Shockley and Hans J. Queisser.

 

[Delta2]

This integral doesn't have a closed form. You can check the indefinite integral at wolfram https://www.wolframalpha.com/input/?i=integral+x^2/(e^x-1)+dx
However :
If $x_g$ is larger than 1, then you can approximate the original integral by the integral $$\int_{x_g}^{\infty}\frac{x^2}{e^x}dx$$ which has a closed form and it is equal to $$\frac{x_g^2+2x_g+2}{e^{x_g}}$$ (you can compute it by doing integration by parts).

The farthest away is $x_g$ from 1, the better this approximation is. For example I found by experimenting at wolfram that for $x_g\geq 5$ the approximation agrees to the original value (which wolframs computes with numerical integration) in the first 3 significant digits.

 

[Max Loo Pin Mok]

Thanks, I'll look at the results from Wolfram Alpha.