- #1
How Do You Calculate Point P3 in a Coordinate System with a 90-Degree Angle?
- Thread starter chuyler1
- Start date
-
- Tags
- Coordinate
Click For Summary
Discussion Overview
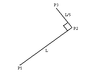
The discussion revolves around calculating the coordinates of point P3 in a coordinate system where a 90-degree angle is formed between the lines connecting points P1, P2, and P3. The problem involves determining the relationship between these points given specific distance constraints.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
Main Points Raised
- One participant seeks to find the equation for point P3 based on known points P1 and P2, specifying that the distance from P2 to P3 should be 1/5 the distance from P1 to P2.
- Another participant suggests showing previous attempts to clarify where assistance is needed.
- A participant expresses uncertainty about how to start and mentions a potential simplification by adjusting P2's y-coordinate, although this may not yield accurate results in all cases.
- One participant proposes using the property of slopes of perpendicular lines, indicating that the slopes of the lines connecting the points are negative reciprocals.
- Clarification is sought regarding the definitions of the slopes m1 and m2 in the context of the problem.
- A participant asserts that vector algebra can be used instead of calculus and questions whether the line P1-P2 could be vertical.
- Another participant confirms that they are open to using trigonometric functions in their solution.
- A later reply suggests that trigonometric functions may not be necessary and provides a method to calculate the coordinates of P3 using similar right triangles and a scale factor.
- One participant confirms that the proposed method for calculating P3's coordinates works perfectly.
Areas of Agreement / Disagreement
While there is some agreement on the approach to finding point P3, multiple methods and perspectives are presented, indicating that the discussion remains somewhat unresolved with respect to the best approach.
Contextual Notes
Participants express varying levels of familiarity with calculus and trigonometry, which may influence their proposed methods. The problem's complexity and the need for efficiency in calculations are also noted.
- #2
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
Welcome to PF!
Hi chuyler1! Welcome to PF!
Show us what you've tried, and where you're stuck, and then we'll know how to help.
Hi chuyler1! Welcome to PF!
Show us what you've tried, and where you're stuck, and then we'll know how to help.
- #3
chuyler1
- 5
- 0
I haven't a clue where to begin. It's been 8 years since the last time I had to think about calculus. I found some equations on how to rotate a point by 90 degrees but the only examples are to rotate around (0,0).
This calculation has to be performed hundreds of times in a short amount of time so if the equation is too complex i may just fudge it by increasing point P2's y by L/5. It simplifies the problem but doesn't provide desirable results in all situations.
This calculation has to be performed hundreds of times in a short amount of time so if the equation is too complex i may just fudge it by increasing point P2's y by L/5. It simplifies the problem but doesn't provide desirable results in all situations.
- #4
- 12,179
- 186
Could you use the fact that the slopes of perpendicular lines are negative reciprocals of each other? I.e.:
m1 = -1/m2
m1 = -1/m2
- #5
chuyler1
- 5
- 0
What is m1 and m2 in your equation?
- #6
- 12,179
- 186
They are the slopes of the two lines you drew.
m1 = slope of line P1-P2
m2 = slope of line P2-P3
m1 = slope of line P1-P2
m2 = slope of line P2-P3
- #7
- 7,399
- 2,927
No calculus is needed here... just vector algebra.
(Will P1-P2 ever be vertical?)
Are you willing to use trig-functions?
(Will P1-P2 ever be vertical?)
Are you willing to use trig-functions?
- #8
chuyler1
- 5
- 0
Yes, P1 and P2 are arbitrary, they could be any angle or even reversed. I have trig functions available to me so a solution involving them isn't a problem.
- #9
- 12,179
- 186
I've had some more time to think about this. We won't even need trig!
In the figure, note that we form two similar right triangles, with a scale factor of 1:5.
To get the x-coordinate of P3, subtract (y2-y1)/5 from x2.
To get the y-coordinate of P3, add (x2-x1)/5 to y2.
In the figure, note that we form two similar right triangles, with a scale factor of 1:5.
To get the x-coordinate of P3, subtract (y2-y1)/5 from x2.
To get the y-coordinate of P3, add (x2-x1)/5 to y2.
- #10
chuyler1
- 5
- 0
Awesome! Works perfectly!
Similar threads
- · Replies 7 ·
- · Replies 5 ·
- · Replies 4 ·
- · Replies 9 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 1 ·