How Do You Calculate Sound Speed with Changing Path Length Interference?

[kris24tf]

Sound Waves Problem and I'm Stuck! Please Help!

Linear Superposition

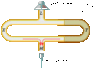
The sound produced by a loudspeaker has a frequency of 12,000 Hz and arrives at the microphone via two different paths. The sound travels through the left tube LXM, which has a fixed length. Simultaneously, the sound travels through the right tube LYM, the length of which can be changed by moving the sliding section. At M, the sound waves coming from the two paths interfere. As the length of the path LYM is changed, the sound loudness detected by the microphone changes. When the sliding section is pulled out by 0.020 m, the loudness changes from a maximum to a minimum. Find the speed at which sound travels through the gas in the tube.


Yeah, so right now I understand that if the loudness goes from a maximum to a minimum, the interference condition changes from constructive interference to destructive interference.
When the sliding section is pulled out, the path difference changes by lambda/2, which does not have the same value as the distance the sliding section moves.

I am not sure where to begin. It seems like a changing variable question mixed with a straightforward question. If anyone could get me going I would appreciate it.

 

[jtbell]

When the sliding section is pulled out, the path difference changes by lambda/2, which does not have the same value as the distance the sliding section moves.

It seems that a diagram (not shown here) accompanies this problem. Can you use that diagram to determine the relationship between the change in the path difference and the distance the sliding section moves? If so, you should be able to calculate the wavelength (lambda).

You're given the frequency. How do you find the speed of a wave, if you know its frequency and wavelength?

 

[phoenix9]

I also am assigned this problem tonight (though with different numbers)

there is in fact a diagram that accompanies it:

It looks to me that the curve of the sliding section has the same curvature as the static section .. thus one only has to consider distance to get to the curve and distance to return .. thus it seems to me that moving the slide out 0.020m would increase distance traveled by 0.040m .. this would, if your and my logic is correct, make the wavelength 0.080m ..

then just use
v = \lambda f

~Phoenix9