SUMMARY
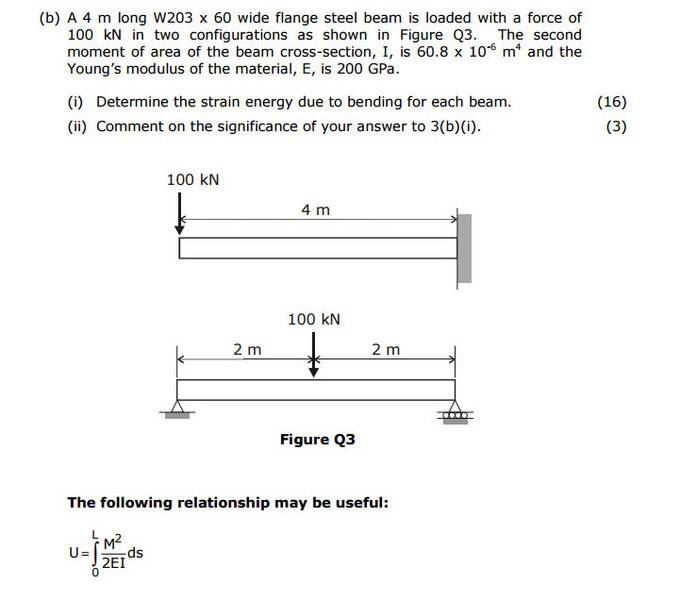
The calculation of strain energy in beams using integral equations requires understanding the bending moment function M(s) with respect to the beam's length coordinate. The strain energy U is defined by the integral U = ∫(M²(s)/(2EI)) ds, where EI is the flexural rigidity. For accurate results, M(s) must be squared term-by-term based on the bending moment diagram, which varies along the length of the beam. The correct application of this method resolves discrepancies in calculated strain energy, as demonstrated in the discussion.
PREREQUISITES
- Understanding of bending moment diagrams
- Familiarity with integral calculus
- Knowledge of beam theory and flexural rigidity (EI)
- Ability to derive M(s) for different loading conditions
NEXT STEPS
- Study the derivation of bending moment functions for various beam types
- Learn how to construct and interpret bending moment diagrams
- Explore advanced integral calculus techniques for evaluating definite integrals
- Investigate the effects of varying load conditions on strain energy calculations
USEFUL FOR
Structural engineers, civil engineering students, and professionals involved in beam analysis and design will benefit from this discussion, particularly those focused on calculating strain energy in structural components.