How Do You Calculate the Probability of a Rat Being in Room 4 After Two Moves?

[JeffNYC]

I've attached the diagram of 4 rooms, which a rat must move through. Each period he changes his room (his state). As you can see if you click on the image, the rat cannot access room 2 from 3, vice versa.

If I assume the rat begins in room 1, how do I calculate the probability he will be in room 4 after his second move? I have the transitional probability matrix correct, I'm just not sure how to move forward.

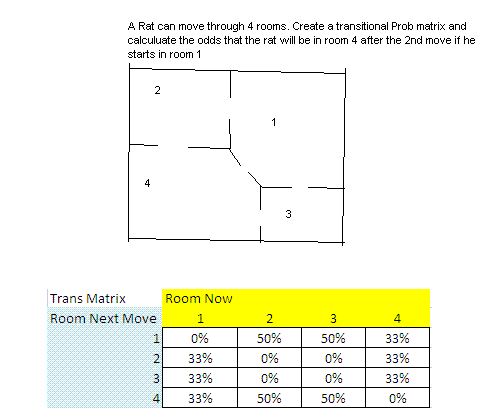
Thank you,

Jeff

 

[HallsofIvy]

Set up the "transition matrix". According to your picture, if the rat is in room 1, the is a 1/3 chance he will move to each of 2, 3, 4. That means you want your first column to be [0 1/3 1/3 1/3]. That's because you will be multiplying the matrix by a column matrix with entries representing the probability the rat is in room 1, 2, 3, or 4 respectively. If you know for certain the rat is in room 1, then your column matrix is [1 0 0 0] and it is the first column of the matrix that multiplies that first 1.

Similarly, if the rat is in room 2 the probability is 1/2 that it will move to room 1 and 1/2 that it will move to room 4: the second column in your matrix must be [1/2 0 0 1/2].

If the rat is in room 3 the probability is also 1/2 that it will move to room 1 and 1/2 that it will move to room 4 so your third column is the same as the second column.

Finally, if the rat is in room 3, the probability is 1/3 that it will move to room 1, 1/3 that it will move to room 2, and 1/3 that it will move to room 3 so the fourth column is [1/3 1/3 1/3 0].

Your transition matrix is
$$A= \left[\begin{array}{cccc} 0 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & 0 \frac{1}{2} \\ \frac{1}{2} & 0 & 0 \frac{1}{2} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0\end{array}\right]$$

Is that what you have?

To find "the probability he will be in room 4 after his second move If the rat begins in room 1" you need to calculate A² times the column matrix [1 0 0 0].

 

[JeffNYC]

Thanks - that's what I thought, but I wasn't sure about the treatment of the initial probability vector.

Jeff