This is an old thread that was left hanging (no final solution to the posed problem). Let's take a stab at solving it, as the solution is unlikely to affect the OP's grades at this point

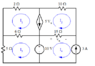
For starters, let's use a more conventional assignment of current directions for the meshes (all clockwise):
By inspection we can see that ##I_4 = -3## (amps).
That's one loop current solved without hardly any effort. We will need three more equations to solve for the other loop currents.
We can incorporate the influence of the known loop 4 current into the circuit by adding a voltage source to the 15Ω branch (there's no shared resistance with loop 3, so no influence there; The 10 V voltage source is a "wall" beyond which loop 4 cannot have any influence).. The 3 amp mesh current of loop 4 will produce a voltage drop of 3*15 = 45 V across the 15Ω resistor, driving a current counterclockwise in that loop (so the source will have the same polarity as ##v_x## in the diagram). That's the voltage source we need to introduce into that branch to account for ##I_4##. Now we can forget loop 4 and concentrate on the rest of the circuit.
The controlled current source between loops 1 and 2 informs us that we should employ a supermesh. A suitable supermesh would encompass loops 1 and 2. So, writing mesh equations:
We also have to consider the auxiliary, or constraint equations imposed by the controlled current source. So:
So by the constraint equations we find:
If we clean up the equations a bit we now have:
Three equations in three unknowns.
From the three equations we can write the impedance matrix and voltage vector:
A person without a computer would likely employ Cramer's Rule or back-substitution or some other method to solve the system of equations. A person with a computer can do the same but without the brain-sweat.
Hence:
Translate the current values with our clockwise direction definition to the original circuit diagram's current direction definitions and you're done. Here's the original circuit drawing: