How does a rigid block on its edge move?

[tmiddlet]

I am self studying physics, and a problem that I have not been able to figure out has been bothering me.
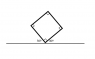
Look at the image (also attached): http://imgur.com/xHP2S"

Let's say that the side length is 1 m. and the mass is 10kg. The object has no initial velocity and assume there is infinite friction with the ground and that the only other force is gravity (9.8 m/s/s)

I've been trying to see how to predict its motion, but I can't see a good way to keep track of how the center of mass and the bottom angles are changing.

I'm not necessarily looking for the answer to this problem, but I want to know how this kind of thing works in general.

 

[tiny-tim]

welcome to pf!

hi tmiddlet! welcome to pf!

… I can't see a good way to keep track of how the center of mass and the bottom angles are changing.

by "infinite friction", do you mean that the bottom point is stationary?

if so, i don't see the difficulty …

the slope of the line from the bottom to the centre of mass is 45° more than the slope of one side

 

[tmiddlet]

Maybe I haven't reached the appropriate topic yet, but what I want to see is how the object rotates about the stationary point due to gravity. By infinite friction I mean the bottom point is stationary, does not slide.

 

[tiny-tim]

Maybe I haven't reached the appropriate topic yet …

if you haven't done moment of inertia you won't be able to do this

if you have, then just use conservation of energy ​

 

[tmiddlet]

I calculated the moment of inertia to be 5, but I'm not sure how to use conservation of energy because I don't know how to calculate gravitational potential energy on this object.

 

[tiny-tim]

hi tmiddlet!

gravitational potential energy of any body is just mgh where m is the total mass and h is the height of the centre of mass