Michal Fishkin
- 8
- 1
Hi! I am new to the forums and this is my first question.
I am investigating the properties of this type of chain.

In order to understand it better, I need to know the physics behind a falling angled rod.
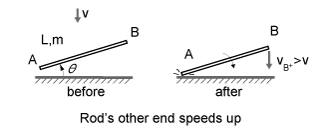
I understand that the other end speeds up to conserve momentum, but I do not understand how to calculate it. The paper I read on it stated that
What would be the derivation behind the 50% increase in speed?
Are there other important aspects I am missing?
Does the angle affect the velocity?
Thank you in advance!
I am investigating the properties of this type of chain.
In order to understand it better, I need to know the physics behind a falling angled rod.
I understand that the other end speeds up to conserve momentum, but I do not understand how to calculate it. The paper I read on it stated that
If one let's a tilted rod fall onto a table, its other end speeds up on hitting (by 50% for a uniform rod with small θ having plastic impact: VB+ = 3V/2).
I also understand that for very small angles and lengths I could assume that end B is traveling in a straight line.What would be the derivation behind the 50% increase in speed?
Are there other important aspects I am missing?
Does the angle affect the velocity?
Thank you in advance!