Benjamin_harsh
- 211
- 5
- Homework Statement
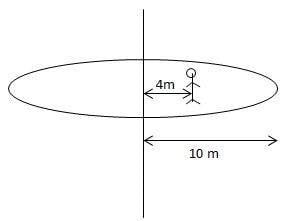
- A 500kg merry go round with a radius of 10m is moving at a speed of 0.5 rad\sec. A 40kg child jumps on the merry-go-round at a position of 4m away from the center of rotation. (a) What is the inertia of the merry-go-round? (b) What is the inertia of the child on the merry-go-round? (c) What is the final speed of the merry-go-round when the child jumps on it?
- Relevant Equations
- ##L_{0} = L_{f}##
Sol:
a) inertia of the merry-go-round(disc) = ##\large\frac{1}{2} \normalsize MR^{2} = \large\frac{1}{2}\normalsize(500)(10^{2}) = 25000 kgm^{2}##
b) inertia of the child who jumped on the merry-go-round = ##MR^{2} = (40)42 = 640 kgm^{2}##
c) final speed of the merry-go-round when the child jumps on it: ##L_{0} = L_{f}##
##I_{M}ω_{0} = I_{C+M}ω_{F}##
##25000(0.5) = 25640.ω_{F}##
##ω_{F} = 0.488 rad\sec##
How ##L_{0} = L_{f}##?
a) inertia of the merry-go-round(disc) = ##\large\frac{1}{2} \normalsize MR^{2} = \large\frac{1}{2}\normalsize(500)(10^{2}) = 25000 kgm^{2}##
b) inertia of the child who jumped on the merry-go-round = ##MR^{2} = (40)42 = 640 kgm^{2}##
c) final speed of the merry-go-round when the child jumps on it: ##L_{0} = L_{f}##
##I_{M}ω_{0} = I_{C+M}ω_{F}##
##25000(0.5) = 25640.ω_{F}##
##ω_{F} = 0.488 rad\sec##
How ##L_{0} = L_{f}##?