How Does Conservation of Momentum Apply in a Frictionless Wagon-Body System?

[Eitan Levy]

Homework Statement

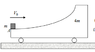
Everything we know is in the picture.
There is no friction between the body and the wagon and between the wagon and the floor.
What will be the maximum height that the body will reach on the wagon? (Answer:0.008v₀²)
What will be the velocities of the body and the wagon once the body reaches A again? (Answer:-v₀, 0.4v₀).

Homework Equations

m₁v₁+m₂v₂=m₁u₁+m₂u₂
0.5m₁v₁²+0.5m₂v₂²=0.5m₁u₁+0,5m₂u₂²

The Attempt at a Solution

I tried applying conservation of momentum and conservation of energy to solve both of them.
For the second question:
mv₀=mu₁+4mu₂
0.5mv₀²=0.5mu₁²+2mu₂²
Which gives incorrect answer, and if we look at the answers both of conservation of energy and conservation of momentum don't apply here.
Why? How can I solve this?

 

[dRic2]

I think you should consider also the potential energy ($mgh$) in your equations

$\frac 1 2 m v_1^2 +mgh_0 = \frac 1 2 M u_2^2 + mgh_1$

You can set $h_0 = 0$ and solve the equation together with the conservation of momentum

 

[Eitan Levy]

I think you should consider also the potential energy ($mgh$) in your equations

$\frac 1 2 m v_1^2 +mgh_0 = \frac 1 2 M u_2^2 + mgh_1$

You can set $h_0 = 0$ and solve the equation together with the conservation of momentum

I said that h_A=0, so how is this relevant here? Both the wagon and the body are at the same height they were at first.

 

[dRic2]

$h_A$ is my $h_0$ and of course is 0, but $h_1$ is not 0

 

[Eitan Levy]

$h_A$ is my $h_0$ and of course is 0, but $h_1$ is not 0

Of course, but the equations I wrote were about the second question, not the first one.

 

[dRic2]

But the energy equation doesn't change, you have to use potential energy also in the second question

 

[dRic2]

For the second question the equation should be $mgh + \frac 1 2 M u_2^2 = \frac 1 2 m v_f^2 + \frac 1 2 M u_f^2$

 

[BvU]

Everything we know is in the picture

Always good to check such a statement. So nothing happens ? Or does the cart make a stop and then mass $m$ shoots for- and upward ?

 

[Eitan Levy]

Always good to check such a statement. So nothing happens ? Or does the cart make a stop and then mass $m$ shoots for- and upward ?

"A wagon with a mass of 4m is capable of moving on a horizonal surface. A body with the mass of m is given a velocity of v₀ while the wagon has no velocity. There is no friction between the wagon, the floor and the body.
What will be the maximum height that the body will reach on the wagon? (Answer:0.008v02)
What will be the velocities of the body and the wagon once the body reaches A again? (Answer:-v0, 0.4v0).

 

[Orodruin]

(Answer:0.008v02)

This cannot possibly be a correct answer. The dimensions are wrong.

(Answer:-v0, 0.4v0)

This is also obviously wrong as it would mean energy was created in the collision.

mv0=mu1+4mu2

What is the relation between $u_1$ and $u_2$ when the box is at the highest point?

0.5mv02=0.5mu12+2mu22

This equation is missing something.

 

[Eitan Levy]

This cannot possibly be a correct answer. The dimensions are wrong.

This is also obviously wrong as it would mean energy was created in the collision.What is the relation between $u_1$ and $u_2$ when the box is at the highest point?This equation is missing something.

The equations were for the time that the body goes through A again, not for the time in which he was at the highest point.
I thought that the velocity of the body when he reaches its highest point is zero.
Perhaps they are equals so that the body doesn't move in relative to the wagon at its highest point? Not sure.

 

[Orodruin]

I thought that the velocity of the body when he reaches its highest point is zero.
Perhaps they are equals so that the body doesn't move in relative to the wagon at its highest point? Not sure.

One of these is correct. What would happen if the velocity of the box was zero when it reached the highest point and the wagon was moving with some other velocity?

The equations were for the time that the body goes through A again, not for the time in which he was at the highest point.

For the second question it should give you the correct answer. As I said, the answer you were given is obviously wrong.

 

[Eitan Levy]

One of these is correct. What would happen if the velocity of the box was zero when it reached the highest point and the wagon was moving with some other velocity?For the second question it should give you the correct answer. As I said, the answer you were given is obviously wrong.

I am not really sure. The wagon will move away from the body? I have no idea what would exactly happen.

 

[Orodruin]

I am not really sure. The wagon will move away from the body? I have no idea what would exactly happen.

If you consider the rest frame of the wagon, what is the velocity of the box at the highest point, i.e., where it turns around?

 

[Eitan Levy]

If you consider the rest frame of the wagon, what is the velocity of the box at the highest point, i.e., where it turns around?

I guess that because we know that their velocities are equal when it turns around we can calculate this. However, I have no idea why is that the case.

 

[Orodruin]

I guess that because we know that their velocities are equal when it turns around we can calculate this. However, I have no idea why is that the case.

Why the velocities are equal at the turnaround? The box moves along a fixed trajectory in the rest frame of the wagon. It needs to have velocity zero when it turns around, there is no other way of turning around.

 

[Eitan Levy]

Why the velocities are equal at the turnaround? The box moves along a fixed trajectory in the rest frame of the wagon. It needs to have velocity zero when it turns around, there is no other way of turning around.

I mean why the relative velocity is zero and not the velocity of the box. Why, as you suggested, the wagon can't move with some other velocity, the body won't just fall down? Or maybe this is correct theoretically but in reality this situation cannot happen because the relative velocity will be zero before we reach this situation?

 

[haruspex]

I guess that because we know that their velocities are equal when it turns around we can calculate this. However, I have no idea why is that the case.

In the rest frame of the wagon: if the body is moving then, since the gradient is nowhere zero, it is either rising or falling. So either it has yet to reach its highest point or it reached it earlier. At the highest point it is, instantaneously, neither rising nor falling, so is not moving relative to the wagon. So at this point they have the same velocity in the ground frame.

 

[haruspex]

(Answer:0.008v02)

It would seem that "g" has been replaced by "10", i.e. that the given answer is supposed to be 0.08v₀²/g. That is wrong. Somebody erred in cancelling a factor (m+M). The correct answer is $\frac{v_0^2M}{2g(M+m)}$, where in this case M=4m, so becomes 0.4v₀²/g.
If we replace g by 10m/s² that becomes 0.04v₀²s²/m. Note the units.

 

[haruspex]

(Answer:-v0, 0.4v0).

As Orodruin notes, that is impossible. -v₀ would be the relative velocity. In the ground frame the velocities will be -0.6v₀ and 0.4v₀.

 

[Eitan Levy]

Another thing I don't understand is why this system is considered to be close (why it is possible to use conservation of momentum). Isn't gravity considered to be an external force?

 

[gneill]

Another thing I don't understand is why this system is considered to be close (why it is possible to use conservation of momentum). Isn't gravity considered to be an external force?

There's no motion (by the wagon) in the vertical direction, so no energy can be lost that way. The motions are frictionless in the horizontal direction, so no energy loss that way either.

 

[Eitan Levy]

There's no motion (by the wagon) in the vertical direction, so no energy can be lost that way. The motions are frictionless in the horizontal direction, so no energy loss that way either.

But what about the vertical motion of the body? Doesn't gravity do work on it?

 

[gneill]

But what about the vertical motion of the body? Doesn't gravity do work on it?

Sure, and it's returned when the block descends again. If you think about it, the gravitational potential is behaving like a spring, storing the energy of "collision" and returning it. You could answer the second part of the problem by considering the scenario as a perfectly elastic collision between the block and wagon.

 

[Eitan Levy]

Sure, and it's returned when the block descends again. If you think about it, the gravitational potential is behaving like a spring, storing the energy of "collision" and returning it. You could answer the second part of the problem by considering the scenario as a perfectly elastic collision between the block and wagon.

Just to make sure, I can use momentum conservation because at the end of the day, the total work of gravity on the body equals to zero?

 

[gneill]

Just to make sure, I can use momentum conservation because at the end of the day, the total work of gravity on the body equals to zero?

Yes, that and there are no frictional losses.

 

[Orodruin]

Just to make sure, I can use momentum conservation because at the end of the day, the total work of gravity on the body equals to zero?

No. You are using momentum conservation in the horizontal direction only. Gravity works vertically by definition of "vertical". The momentum of the system in the vertical direction is not conserved during the collision (even though it is zero both at the beginning and at the end, it will be non-zero as the box moves up. Hence, the correct argument is that you can use momentum conservation in the horizontal direction because there are no forces acting on the system in this direction.

As for energy conservation, see the replies by @gneill