How Does Friction Affect the Motion of a Uniform Rod Released at an Angle?

[Telemachus]

Homework Statement

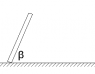
A uniform rod of mass m and length L is released from rest when the angle $$\beta$$ is 60º. If the friction between the bar and the surface is such that prevent slippage of the same get:
a. The angular acceleration of the bar when set free.
b. The contact force N and friction in A (A is the contact point.)
c. The minimum coefficient of friction to ensure the movement.

The Attempt at a Solution

I did as follows:
a.
$$I_y=\displaystyle\frac{mL^2}{3}$$

$$I_y\alpha=mg \cos \beta$$
$$\alpha=\displaystyle\frac{3g\cos\beta}{2L}$$

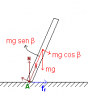
b. Here arises a force diagram as follows, and is where the doubts appear.

$$N=mg$$
Then:

$$mg \cos \beta \cos 30º-mg \sin \beta\cos 30º-f_r=0$$
$$f_r=mg \cos 30º(\cos \beta - \sin \beta)$$
Is this correct?

Greetings and thanks.

 

[Telemachus]

I think its wrong, and that $$N=mg \sin \beta$$ but I'm not sure. I did this looking at an example of physics pendulum, analogue to the forces produces over the axis of rotation, but I'm not sure if this is right.

 

[Telemachus]

Now I did this:

$$N_x-mg\cos\beta=m\displaystyle\frac{L}{2}\ddot \theta$$

$$N_y-mg\sin\beta=m\displaystyle\frac{L}{2}\dot \theta^2$$

With $$\ddot \theta=\alpha\longrightarrow{N_x=\displaystyle\frac{3}{4}mg\cos \beta}$$
Its released from rest, then $$\dot \theta=0\longrightarrow{Ny=mg\sin \beta}$$

Then $$N=N_x \hat{i}+N_y \hat{j}$$

$$|N|=\sqrt[ ]{N_x^2+N_y^2}=\sqrt[ ]{\displaystyle\frac{9}{16}m^2g^2\cos^2\beta+m^2g^2\sin^2\beta}$$

I'm not sure about this neither :P

 

[Telemachus]

I did the following, I think this a bit better than before, but I still not sure.

$$r\alpha=a_{cm}\Rightarrow{a_{cm}=\displaystyle\frac{L}{2} \displaystyle\frac{3g\cos\beta}{2L}}$$

Where we recall that $$\alpha=\displaystyle\frac{3g\cos\beta}{2L}$$ and $$\beta=60º$$

What gives $$a_{cm}=\displaystyle\frac{3}{8}g$$

Then: $$N-mg=ma_{cm}\longrightarrow{N=\displaystyle\frac{3}{8}mg-mg=-\displaystyle\frac{5}{8}mg}$$

Now what did I do with the friction force was to use the moment equation.

$$f_r\cos 30º\displaystyle\frac{L}{2}=I_{cm}\alpha\Rightarrow{f_r=\displaystyle\frac{2I_{cm}\alpha}{L\cos 30º}}=\displaystyle\frac{mg}{4\sqrt[ ]{3}}$$

Anyone?

 

[Telemachus]

I have realized that what I've done before it's all wrong. Let's see now.

$$x_{mc}=\displaystyle\frac{L}{2}\cos \beta$$

$$y_{mc}=\displaystyle\frac{L}{2}\sin \beta$$
$$\dot y_{mc}=\displaystyle\frac{L}{2}\cos \beta\dot\beta$$
$$\ddot y_{mc}=-\displaystyle\frac{L}{2}\sin \beta\dot\beta^2+\displaystyle\frac{L}{2}\cos\beta\ddot\beta$$Then:
$$N-mg=ma_{y_{mc}}$$
Then $$N=m\left (-\displaystyle\frac{L}{2}\sin \beta\dot\beta^2+\displaystyle\frac{L}{2}\cos\beta\ddot\beta \right) +mg$$

Then the friction force can be obtained from the moment equation respect to the mass center
$$(f_r\sin\beta+N\cos\beta)\displaystyle\frac{L}{2}=I_{mc}\alpha$$

Is this right? somebody?

Greetings.

*mc refers to the mass center.