shalikadm
- 63
- 0
I am trying to figure out what happens here...and now I've stuck on this...
Here it goes...,
situation 1
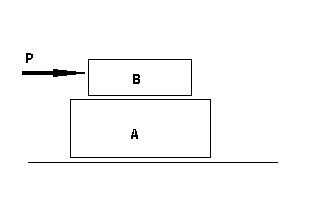
Both contact A with B and A with ground are rough
We increase the force P applied here from zero.When there's sufficiently big μs between A and B than that of A and ground,there's an ability there to move both A and B together at the same speed.What I see here is that there's a friction there even they are moved by the force at a regular velocity.When A travels at a regular speed there must be a force applied on this to cancel out the friction on A by the ground.Actually its the friction applied by B on A that cancels out the friction by ground on A.So there must be a friction between A and B when even traveling at a regular velocity.Am I correct ?
situation 2
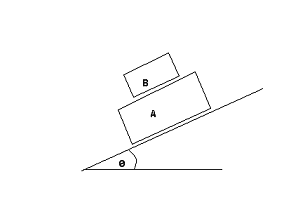
Contact of A with B are rough.BUT A with ground is smooth.
A and B is put in a smooth slope as shown in the image.When we take both A and B together as a one system,there's no friction (friction s between A and B cancels when taken together as one system). So the only force is the resolution of weight parallel to the slope.So the acceleration on this system is gsinθ..Here's where I can't proceed on.We have told that there isn't a friction between A and B when they are going down the slope.The reason that was told for this is that the resolution of weight of B parallel to the slope is used for to keep the gsinθ acceleration parallel to the slope.So there's no any effort of B to slide on A-so there's no friction between them.But to explain this to my self I want to know that B 's acceleration is gsinθ.Is there someone who can explain me how B get an acceleration of gsinθ.I'm afraid to think that the acceleration of B is same as the whole system..I see acceleration is a vector...so aA+aB=asystem like thing is haunting my mind...We see such things in vectors like momentum...momentums of objects of a system is added to the momentum of system (algebraically as a vector)..So in bomb explosion the momentum of the system is zero...like that thing...please explain this to me...
Please try to give me a short and clear explanation(a best one)..
I'm in a hurry
Thanks !
Here it goes...,
situation 1
Both contact A with B and A with ground are rough
We increase the force P applied here from zero.When there's sufficiently big μs between A and B than that of A and ground,there's an ability there to move both A and B together at the same speed.What I see here is that there's a friction there even they are moved by the force at a regular velocity.When A travels at a regular speed there must be a force applied on this to cancel out the friction on A by the ground.Actually its the friction applied by B on A that cancels out the friction by ground on A.So there must be a friction between A and B when even traveling at a regular velocity.Am I correct ?
situation 2
Contact of A with B are rough.BUT A with ground is smooth.
A and B is put in a smooth slope as shown in the image.When we take both A and B together as a one system,there's no friction (friction s between A and B cancels when taken together as one system). So the only force is the resolution of weight parallel to the slope.So the acceleration on this system is gsinθ..Here's where I can't proceed on.We have told that there isn't a friction between A and B when they are going down the slope.The reason that was told for this is that the resolution of weight of B parallel to the slope is used for to keep the gsinθ acceleration parallel to the slope.So there's no any effort of B to slide on A-so there's no friction between them.But to explain this to my self I want to know that B 's acceleration is gsinθ.Is there someone who can explain me how B get an acceleration of gsinθ.I'm afraid to think that the acceleration of B is same as the whole system..I see acceleration is a vector...so aA+aB=asystem like thing is haunting my mind...We see such things in vectors like momentum...momentums of objects of a system is added to the momentum of system (algebraically as a vector)..So in bomb explosion the momentum of the system is zero...like that thing...please explain this to me...
Please try to give me a short and clear explanation(a best one)..
I'm in a hurry
Thanks !