How does Lanchester's transporter work in a curved manifold?

[rbwang1225]

In A Short Course in General Relativity, Forster and Nightingale, page 236, it describes how the Lanchester's transporter operates.

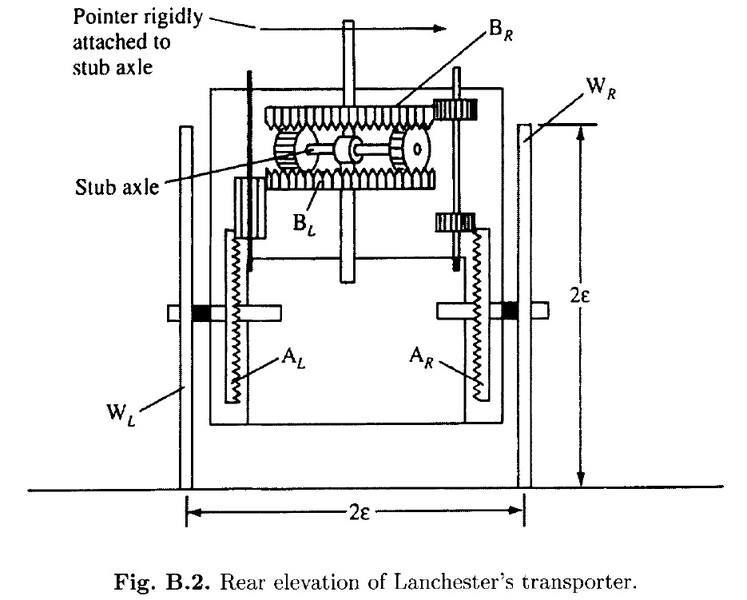
According to the diagram, I think the pointer would turn clockwise when the Lanchester's transporter travels a right-hand bend, however, the paragraph said it rotates anticlockwise.
Second, why is there a one half in the expression of the angle of rotation? Is it because there are "two" pinions?

Any help would be appreciated!

 

[HallsofIvy]

If the "transporter" is turning to the right, its outer wheel, on the left turns faster which means that the lower of the two horizontal cogs turns faster. It, and so the pointer, will turn counterclockwise. And, yes, the "1/2" is there because of there are two wheels- the turning of the pointer is, as shown, the average of the two wheels.

By, the way, I see that this is from a book general relativity, but does this "transporter, itself, have anything to do with "relativity"?

 

[yuiop]

If it helps any, the pointer stub axle is fixed to the central horizontal stub axle, although that is not immediately apparent from the diagram. I assume the purpose of the device is to accurately parallel transport a vector over a curved manifold?