How Does Mass and Inertia Affect Acceleration on an Inclined Plane?

[ASUengineer16]

Homework Statement

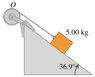
A block with mass m = 5.00 kg slides down a surface inclined 36.9 degrees to the horizontal (the figure View Figure ). The coefficient of kinetic friction is 0.23. A string attached to the block is wrapped around a flywheel on a fixed axis at O. The flywheel has mass 28.0 kg and moment of inertia 0.500 kg*m^2 with respect to the axis of rotation. The string pulls without slipping at a perpendicular distance of 0.200 m from that axis.

Homework Equations

I tied solving for the sum of torques, which is T*r=I*($$\alpha$$) where T is the tension and r is the radius of the pulley, .200 m. I think solved for T for the box. Once solving for T I got, T=mg(sin(theta)-cos(theta)*$$\mu$$k)-m*a. Then using the rule, $$\alpha$$=a/r, I then substituted a/r for all the $$\alpha$$'s and then plugged my T for the torque equation into the T from the force equation.

In the end I came up with the equation:
mg(sin(theta)-cos(theta)*$$\mu$$k)-m*a = (I*a)/r^2

This yeilded me the wrong answer and I have no idea where I am wrong. I have a feeling it has to do with the mass of the pulley since it was given, but I am not sure how to relate it to the problem since they give you the moment of inertia for the pulley ?

Any help would be great thanks !

 

[alphysicist]

Hi ASUengineer16,

What wrong answer did you get?

 

[ASUengineer16]

After solving for a in the final equation I got 1.1 m/s^2

 

[ASUengineer16]

actually seems like I made a rounding error, the correct answer was 1.165 m/s^2 but it wouldn't take 1.1 when I entered it,

and for part b, 14.6 N came out to be correct with 1.2 m/s^2 as the acceleration.

 

[alphysicist]

I was about to write back that I kept getting 1.16619 for the acceleration.

Glad it worked out.