How does multiplying by delta theta relate to spherical coordinates?

[tmbrwlf730]

Hi,

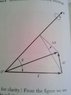
I'm reading through one of my books and it's explaining how a vector is eqaul to multiplying sin\phi and \Delta\vartheta. the way it's written in the text is as followed,

|\Deltai| \approx (sin\phi)\Delta\vartheta

I have never understood how things like this work. Could someone please explain to me why this is true and how it works? I included a picture of the figure it uses. Thank you.

 

[HallsofIvy]

You are talking about spherical coordinates, right? Also you are using "physics" notation which switches \theta and \phi from "mathematics" notation. In your notation, \phi is the "longitude" and \theta is the "co-latitude".

In these coordinates, for a fixed \theta[/tex] and r, sweeping \phithrough 0 to 2\pi, the point (r, \phi, \theta) sweeps through a circle, but not a circle of radius r. If we draw the vertical axis, the line from (0, 0, 0) to the point (r, \phi, \theta), and the line from that point perpendicular to the vertical axis, we get a right triangle with hypotenuse of length r and base angle of \phi. If we call the opposite side to that angle "x" then sin(\phi)= x/r so x= r sin(\phi). That will be the radius of the circle swept out.