How Does Self Inductance Affect Current Over Time in an R-L Circuit?

[TFM]

Homework Statement

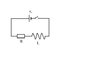
Give a definition of (self) inductance. Suppose a battery, which supplies a constant EMF ϵ_0 is connected to a circuit of resistance R and inductance L at t = 0. Find an expression for the current as a function of time.

Homework Equations

V = IR

[tex]V = -L\frac{dI}{dt} [/tex<br /> <br /> <h2>The Attempt at a Solution</h2><br /> <br /> I am assuming that this is to be treated as a Kirchoff Loop, thus the total voltage = 0<br /> <br /> <i> Voltage providers: </i><br /> <br /> Inductor<br /> Battery<br /> <br /> <i> Users: </i><br /> <br /> Resistor<br /> <br /> Thus I have the equation:<br /> <br /> $$\epsilon - L\frac{dI}{dt} - IR = 0$$<br /> <br /> and thus:<br /> <br /> $$\epsilon - L\frac{dI}{dt} = IR$$<br /> <br /> treating like a differential equation:<br /> <br /> $$\epsilon - L\frac{dI}{dt} = IR$$<br /> <br /> $$\epsilon dt - L dI = IR dt$$<br /> <br /> rearrange:<br /> <br /> $$\frac{L}{IR} dI = -dt + \epsilon dt$$<br /> <br /> Gives:<br /> <br /> $$\frac{1}{L}ln(IR) dI = -t + \epsilon t$$<br /> <br /> multiply by L<br /> <br /> [tex]ln(IR) = -Lt + \epsilon t [/tex<br /> <br /> take exponentials:<br /> <br /> $$IR = e^{-Lt} + e^{\epsilon t}$$<br /> <br /> Does this look right so far?<br /> <br /> TFM[/tex][/tex]

 

[alphysicist]

Hi TFM,

The Attempt at a Solution

I am assuming that this is to be treated as a Kirchoff Loop, thus the total voltage = 0

Voltage providers:

Inductor
Battery

Users:

Resistor

Thus I have the equation:

$$\epsilon - L\frac{dI}{dt} - IR = 0$$

and thus:

$$\epsilon - L\frac{dI}{dt} = IR$$

treating like a differential equation:

$$\epsilon - L\frac{dI}{dt} = IR$$

$$\epsilon dt - L dI = IR dt$$

rearrange:

$$\frac{L}{IR} dI = -dt + \epsilon dt$$

This equation does not follow from the previous one.

 

[TFM]

No it doesn't

so:

$$\epsilon dt - L dI = IR dt$$

see, I have to rearrange to get I onto the left side.

does this look better:

$$\epsilon dt - L dI = IR dt$$

$$- L dI = IR dt - \epsilon dt$$

$$- L dI = (IR - \epsilon) dt$$

$$- \frac{L}{IR - \epsilon} dI = dt$$

so and so:

$$- \frac{1}{L}ln(IR - \epsilon) = t$$

Does this look better?

TFM

 

[alphysicist]

No it doesn't

so:

$$\epsilon dt - L dI = IR dt$$

see, I have to rearrange to get I onto the left side.

does this look better:

$$\epsilon dt - L dI = IR dt$$

$$- L dI = IR dt - \epsilon dt$$

$$- L dI = (IR - \epsilon) dt$$

$$- \frac{L}{IR - \epsilon} dI = dt$$

I think this part looks okay.

so and so:

$$- \frac{1}{L}ln(IR - \epsilon) = t$$

This isn't quite right. The integration is not right (if you take the derivative of the left side with respect to I you don't get the left side of the previous equation). Also remember that these are definite integrals, so you have to evaluate the limits.

 

[TFM]

Would the limits be for I between 0 and I and for t between 0 and t?

I am not sure how to integrate this, because I thought when you integrated:

$$\frac{1}{x} dx$$

you got:

$$ln(x)$$

and for:

$$\frac{b}{x}$$

where b is a constant, you got:

$$\frac{1}{b}lnx$$

?

TFM

 

[alphysicist]

and for:

$$\frac{b}{x}$$

where b is a constant, you got:

$$\frac{1}{b}lnx$$

No, the integral

$$\int \frac{b}{x} dx \to b \ln x$$
(plus a constant) because in that case the b can come out of the integral (it is not affected by the integration process at all). However, you do have to take into account that the R is multiplying the I.

$$- L\left( \int\limits_0^I \frac{1}{IR - \epsilon} dI \right) = \int\limits_0^t dt$$

 

[TFM]

Okay, so:

$$- L\left( \int\limits_0^I \frac{1}{IR - \epsilon} dI \right) = \int\limits_0^t dt$$

$$-L(ln(IR - \epsilon) - (0R - \epsilon)) = t - 0$$

$$-L(ln(IR - \epsilon - - \epsilon)) = t$$

$$-L(ln(IR)) = t$$

?

TFM

 

[alphysicist]

Okay, so:

$$- L\left( \int\limits_0^I \frac{1}{IR - \epsilon} dI \right) = \int\limits_0^t dt$$

$$-L(ln(IR - \epsilon) - (0R - \epsilon)) = t - 0$$

The R has to be handled like this:

$$\int \frac{1}{IR-\epsilon}\ dI \to \frac{\ln(IR-\epsilon)}{R}$$
(plus the constant).

Also when you go to apply limits,

$$\ln (x)\Big|_{x_0}^{x_f} \neq \ln (x_f - x_0)$$

Instead, it is:


$$\ln (x)\Big|_{x_0}^{x_f} = \ln (x_f) - \ln(x_0)$$

 

[TFM]

Okay, so:

$$- L\left( \int\limits_0^I \frac{1}{IR - \epsilon} dI \right) = \int\limits_0^t dt$$

This will integrate to:

$$-L\left[\frac{ln(IR - \epsilon)}{R}\right]^I_0 = t$$

$$-L \left(\frac{IR - \epsilon}{R} - \frac{0R - \epsilon}{R}\right) = t$$

$$-L \left(\frac{IR - \epsilon}{R} - \frac{- \epsilon}{R}\right) = t$$

does this look better?

?

TFM

 

[alphysicist]

You seemed to have dropped your $\ln$'s when you put in the limits.

 

[TFM]

Sorry, copied through typo

It should be:

$$-L\left[\frac{ln(IR - \epsilon)}{R}\right]^I_0 = t$$

$$-L \left(\frac{ln(IR - \epsilon)}{R} - \frac{ln(0R - \epsilon)}{R}\right) = t$$

$$-L \left(\frac{ln(IR - \epsilon)}{R} - \frac{ln(- \epsilon)}{R}\right) = t$$

?

TFM

 

[TFM]

Does this look correct

?

TFM

 

[alphysicist]

What does that give for I?

 

[TFM]

Well, if we rearrange it:

$$-L \left(\frac{ln(IR - \epsilon)}{R} - \frac{ln(- \epsilon)}{R}\right) = t$$

$$\left(\frac{ln(IR - \epsilon)}{R} - \frac{ln(- \epsilon)}{R}\right) = -\frac{t}{L}$$

Multiply by R:

$$ln(IR - \epsilon) - ln(-\epsilon) = -\frac{Rt}{L}$$

take exponentials:

$$IR - \epsilon + \epsilon = e^{-\frac{Rt}{L}}$$

$$IR = e^{-\frac{Rt}{L}}$$

$$I = \frac{^{-\frac{Rt}{L}}}{R}$$

Does this look correct?

TFM

 

[alphysicist]

Well, if we rearrange it:

$$-L \left(\frac{ln(IR - \epsilon)}{R} - \frac{ln(- \epsilon)}{R}\right) = t$$

$$\left(\frac{ln(IR - \epsilon)}{R} - \frac{ln(- \epsilon)}{R}\right) = -\frac{t}{L}$$

Multiply by R:

$$ln(IR - \epsilon) - ln(-\epsilon) = -\frac{Rt}{L}$$

take exponentials:

$$IR - \epsilon + \epsilon = e^{-\frac{Rt}{L}}$$

This line is not correct, because:

$$\exp \left\{ \ln x + \ln y\right\} \neq x + y$$

Before you take the exponential of both sides, you just want a single natural log on the left . That is, you want the left side to be just:

ln(something)

 

[TFM]

so:

$$ln(IR - \epsilon) - ln(-\epsilon) = -\frac{Rt}{L}$$

isn't $$ln(a) - ln(b) = ln(\frac{a}{b})$$

?

If so:

$$ln(IR - \epsilon) - ln(-\epsilon) \equiv ln\left(\frac{IR - \epsilon}{-\epsilon} \right)$$

giving:

$$ln\left(\frac{IR - \epsilon}{-\epsilon} \right) = \frac{-Rt}{L}$$

taking exponentials:

$$\frac{IR - \epsilon}{-\epsilon} = e^{\frac{-Rt}{L}}$$

Does this look better?

TFM

 

[alphysicist]

Yes.

 

[TFM]

Excellent. So:

$$\frac{IR - \epsilon}{-\epsilon} = e^{\frac{-Rt}{L}}$$

$$IR - \epsilon = \epsilon e^{\frac{-Rt}{L}}$$

$$IR = \epsilon - \epsilon e^{\frac{-Rt}{L}}$$

factorise out:

$$IR = \epsilon \left(1 - e^{\frac{-Rt}{L}} \right)$$

divide by R:

$$I = \frac{\epsilon}{R} \left(1 - e^{\frac{-Rt}{L}} \right)$$

Does this look correct?

TFM

 

[alphysicist]

$$I = \frac{\epsilon}{R} \left(1 - e^{\frac{-Rt}{L}} \right)$$

Does this look correct?

TFM

That looks right to me.