robertjford80
- 388
- 0
This is a screenshot from one of susskind's cosmology lectures.
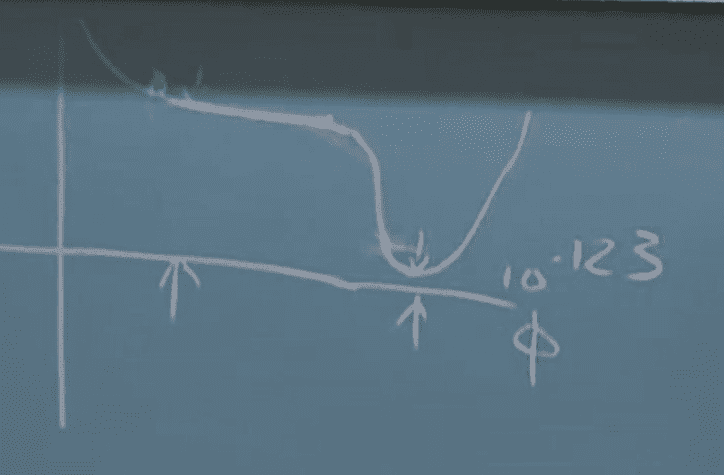
it shows a graph of V(φ). As you can see it slowly rules down then, bam, it rolls really fast down hill. I thought inflation erased all the information before it happened. So how does he know there is a gradual decline before a fast decline?
it shows a graph of V(φ). As you can see it slowly rules down then, bam, it rolls really fast down hill. I thought inflation erased all the information before it happened. So how does he know there is a gradual decline before a fast decline?