I How does the Hall effect interact with the iLB force in a copper wire?

[feynman1]

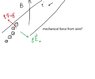
A current is flowing in a copper wire (electrons are flowing). The electrons will be deflected to the left wall of the wire due to Hall effect. They leave on the right wall of the wire a deficit of electrons, leaving them positively charged, so there’s a voltage difference between the left and right. An electric force will act on the electrons on the left.

• Does the electric force 100% cancel the magnetic force qvB?
• If ‘1’ is yes, how does the wire still feel a Laplace force/Ampere force iLB? If ‘1’ is no, does the wall of the wire give the electrons a normal/pulling force to balance them?

 

[Dale]

Is the wire allowed to accelerate under the magnetic force or is it mechanically restrained from accelerating?

 

[feynman1]

Is the wire allowed to accelerate under the magnetic force or is it mechanically restrained from accelerating?

Shall we consider both cases?

 

[Dale]

If the wire is accelerating then the forces are not 100% canceled, and if the wire is not accelerating then the forces are 100% canceled (including the mechanical forces). Both per Newton’s 2nd law.

The second part of your question makes no sense. The fact that a second force cancels out a first force doesn’t get rid of the first force. It never has. If it got rid of the first force then the object would accelerate the opposite direction under the influence of the second force or it would stop experiencing tension or something else equally non-physical.

 

[Delta2]

The electrons that makeup the flow of current, exert on the surface charges that makeup the hall voltage, a total electric force that is equal to BiL, and this force isn't canceled by anything and is what will make the wire move if left unbalanced by an external force.
check this thread and especially post #6 there
https://www.physicsforums.com/threads/hall-voltage-vs-laplace-force.879412/

 

[vanhees71]

The case with the wire fixed in space is easy to calculate, even in full relativistic treatment. One only has to use the correct realtivistic version of Ohm's Law, which automatically takes care of the Hall effect:

https://www.physicsforums.com/insights/relativistic-treatment-of-the-dc-conducting-straight-wire/

 

[feynman1]

If the wire is accelerating then the forces are not 100% canceled, and if the wire is not accelerating then the forces are 100% canceled (including the mechanical forces). Both per Newton’s 2nd law.

The second part of your question makes no sense. The fact that a second force cancels out a first force doesn’t get rid of the first force. It never has. If it got rid of the first force then the object would accelerate the opposite direction under the influence of the second force or it would stop experiencing tension or something else equally non-physical.

I don't get your answer. I was asking if qvB is 100% canceled out by the Hall effect force alone. Of course when in balance the net force is 0.

 

[feynman1]

The electrons that makeup the flow of current, exert on the surface charges that makeup the hall voltage, a total electric force that is equal to BiL, and this force isn't canceled by anything and is what will make the wire move if left unbalanced by an external force.
check this thread and especially post #6 there
https://www.physicsforums.com/threads/hall-voltage-vs-laplace-force.879412/

I thought qvB might be canceled out by the Hall effect electric force and some mechanical contact force from the wall of the wire. But I’m not sure if mechanical forces should be considered on the scale of a wire, since mechanical forces are of EM orgin on a microscopic level.

 

[Dale]

I don't get your answer. I was asking if qvB is 100% canceled out by the Hall effect force alone. Of course when in balance the net force is 0.

Then you should only be interested in the accelerating case, yes? Otherwise there is another force in the mix and you can never assign the cancelation to just one.

 

[feynman1]

Then you should only be interested in the accelerating case, yes? Otherwise there is another force in the mix and you can never assign the cancelation to just one.

I think the equilibrium case will be easier since the net force is 0. If some part of a wire is accelerating, then things get more complex.

 

[Delta2]

I thought qvB might be canceled out by the Hall effect electric force and some mechanical contact force from the wall of the wire. But I’m not sure if mechanical forces should be considered on the scale of a wire, since mechanical forces are of EM orgin on a microscopic level.

We consider the wire not moving. Then qvB is canceled out solely by the Hall effect electric force. The mechanical contact force that prevents the wire from moving is applied to the wall of the wire and not to the free electrons. The mechanical contact force counteracts the force that the stream of free electrons apply to the wall of the wire due to Newton's 3rd law (the surface charges on the wall of wire apply the hall electric force to electrons, hence by Newton's 3rd electrons apply an opposite and equal force to the surface charges on the wall of the wire).

 

[feynman1]

We consider the wire not moving. Then qvB is canceled out solely by the Hall effect electric force. The mechanical contact force that prevents the wire from moving is applied to the wall of the wire and not to the free electrons. The mechanical contact force counteracts the force that the stream of free electrons apply to the wall of the wire due to Newton's 3rd law (the surface charges on the wall of wire apply the hall electric force to electrons, hence by Newton's 3rd electrons apply an opposite and equal force to the surface charges on the wall of the wire).

Thanks. Would drawing a diagram be clearer?

 

[Delta2]

Thanks. Would drawing a diagram be clearer?

I admit that drawing a figure would make the whole thing clearer but I am afraid I am not good on using drawing programs.

 

[feynman1]

I admit that drawing a figure would make the whole thing clearer but I am afraid I am not good on using drawing programs.

‘paint' in win10 will work

 

[Dale]

I think the equilibrium case will be easier since the net force is 0. If some part of a wire is accelerating, then things get more complex.

So then why respond that you wanted to consider both? Please put a little more thought into what you want and write more appropriate OP’s.

 

[vanhees71]

I don't get your answer. I was asking if qvB is 100% canceled out by the Hall effect force alone. Of course when in balance the net force is 0.

As shown in my Insights article in the above discussed case of a DC current through a wire the total force on a charge making up this current is indeed 0. It consists of the magnetic force due to the self-induced magnetic field, an electric force due to the resulting charge separation (Hall effect), and friction forces along the wire. It's very illuminating to derive Ohm's Law from simple classical microscopic models (e.g., the Drude model).

 

[feynman1]

As shown in my Insights article in the above discussed case of a DC current through a wire the total force on a charge making up this current is indeed 0. It consists of the magnetic force due to the self-induced magnetic field, an electric force due to the resulting charge separation (Hall effect), and friction forces along the wire. It's very illuminating to derive Ohm's Law from simple classical microscopic models (e.g., the Drude model).

So are you saying qvB isn't 100% canceled by Hall effect alone? Then could you answer the 2nd OP's question?

 

[vanhees71]

I don't understand how you come to the conclusion that the Hall effect doesn't completely cancel the transverse force. Note that in the electrostatic limit the condition that $\vec{j}=0$ together with the relativistic complete form of Ohm's Law implies that
$$\vec{E}_{\perp}+\frac{\vec{v}}{c} \times \vec{B}=0.$$
This is the (DC) Hall effect.

In longitudinal direction the electric force driving the current is compensated by the frictional forces, so that finally you have $\vec{j}=\sigma \vec{E}_{\parallel}$.

All this refers to the magnetic field induced by the considered current through the wire, and due the Hall effect there's no net force acting on the wire.

Of course, if you add an addional external field you get the usual force on a current-conducting wire in this external field in addition. To get a stationary condition this again has to be compensated again by another force of course.

 

[feynman1]

Which precise question are you referring to. I also don't understand how you come to the conclusion that the Hall effect doesn't completely cancel the transverse force. Note that in the electrostatic limit the condition that $\vec{j}=0$ together with the relativistic complete form of Ohm's Law implies that
$$\vec{E}_{\perp}+\frac{\vec{v}}{c} \times \vec{B}=0.$$
This is the (DC) Hall effect.

In longitudinal direction the electric force driving the current is compensated by the frictional forces, so that finally you have $\vec{j}=\sigma \vec{E}_{\parallel}$.

I was referring the 2nd bullet point of the OP.
How do you have j=0 in a current?
You said: "It consists of the magnetic force due to the self-induced magnetic field, an electric force due to the resulting charge separation (Hall effect), and friction forces along the wire". So with friction along the wire, qvB isn't canceled by Hall force.

 

[vanhees71]

I was referring the 2nd bullet point of the OP.
How do you have j=0 in a current?
You said: "It consists of the magnetic force due to the self-induced magnetic field, an electric force due to the resulting charge separation (Hall effect), and friction forces along the wire". So with friction along the wire, qvB isn't canceled by Hall force.

Sorry, I was too fast sending my response. Now it's in final form. Does this answer your question?

 

[feynman1]

not yet, see the updated pic

 

[vanhees71]

The figure is correct for a wire without an additional external magnetic field.

 

[feynman1]

The figure is correct for a wire without an additional external magnetic field.

Then is there a mechanical force from the wire to help balance the charges?

 

[Delta2]

no magnetic field, no hall effect

@vanhees71 do you imply there is a hall effect due to the magnetic field from the current of the wire itself and not from an external magnetic field?

 

[vanhees71]

I'm implying that there's an intrinsic Hall effect, i.e., the Lorentz force on the current elements due to the magnetic field of all the other current elements around and of course also a Hall effect due to an additional external magnetic field. It's all well explained by the Lorentz-force formula
$$\vec{f}=\vec{E} + \frac{1}{c} \vec{j} \times \vec{B},$$
for the force density. Here $\vec{E}$ and $\vec{B}$ are the total fields, particularly, $\vec{B}=\vec{B}_{\text{self}} + \vec{B}_{\text{ext}}$.