How does the number of turns in a loop affect the torque in a magnetic field?

[estanton]

Homework Statement

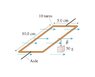
The 10-turn loop of wire shown in the figure lies in a horizontal plane, parallel to a uniform horizontal magnetic field, and carries a 2.0A current. The loop is free to rotate about a nonmagnetic axle through the center. A 50g mass hangs from one edge of the loop.

Homework Equations

Torque = r x F
Torque = IA x B

The Attempt at a Solution

My thought was to simply calculate the torque created by the mass and then relate that with an opposite torque provided by the magnetic field. I suspect that I'm calculating the torque created by the hanging mass wrong, since I haven't really dealt with torques in some time.
Torque = r x F -> .025m*.05kg*9.8m/s^2 = .01225 Nm
Torque = IA x B -> Torque/IA = B -> .01225/(2.0A*(.05*.1)) = B = 1.225 T

If someone could help with what I'm overlooking here I would appreciate it.

 

[estanton]

never mind, I figured out that I have to use N (number of turns) in with mu.

 

[sahar13]

Hey, I tried the same thing you did... how do you factor in the number of turns?

 

[Redbelly98]

Welcome to PF

For a 1-turn loop, the torque is what estanton had before:

T = I AxB​

If instead you have 10 loops, can you tell how that affects the torque?