How Does the Track's Force Affect a Moving Car's Dynamics?

[dvep]

Homework Statement

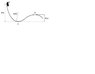
A car weighing 1300 kg starts from rest at point 1, it moves down the track without friction.

1) Determine the force exerted by the track on the car at point 2
2) Determine what the minimum radius at point 3 has to be so that the car does not leave the track.

Figure is attached.

Homework Equations

N = (mv^2)/r + mg

The Attempt at a Solution

By finding the velocity at point 2 and using the equation above ,I have calculated the normal force to be 15855.94 N, is this correct?

For 2, I have calculated the velocity at point 3 to be 12.13 m/s, and am I right to say that the centripetal acceleration must equal gravity so the car does not come off the track.
In this case I calculated the minimum radius to be 1.24 m.
Is this correct?

Thanks.

 

[PhanthomJay]

Your force equatons are correct, but the numerical answers are not...did you calculate the speeds correctly?

 

[dvep]

Your force equatons are correct, but the numerical answers are not...did you calculate the speeds correctly?

I have run through it again
For (1) the velocity i get at point 2 is 18.98 m/s, normal force is 16595.31 N


For (2)

velocity at point 3 i get 16.49 m/s, and the minimum radius i get 1.68 m

 

[PhanthomJay]

I have run through it again
For (1) the velocity i get at point 2 is 18.98 m/s, normal force is 16595.31 N


For (2)

velocity at point 3 i get 16.49 m/s, and the minimum radius i get 1.68 m

Please show your calculations for determining the speed at points 2 and 3. I do not get those numbers.

 

[dvep]

Please show your calculations for determining the speed at points 2 and 3. I do not get those numbers.

1)
centripetal acceleration = v^2/r

velocity at point 2 = sqrt(2*(-9.8^2/6.4)*(-12)) = 18.98 m/s

Normal force = (1300*18.98)/6.4 + 1300*9.8 = 16595.31 N

2) velocity at point 3 = sqrt(-2*(9.8)(4.5)+18.98^2) = 16.49 m/s

r = v^2/g = 16.49^2/9.8 = 16.49^2/9.8 = 27.75 m

I realized I didn't square the velocity on the last bit, though i think it is wrong anyways.

 

[PhanthomJay]

1)
centripetal acceleration = v^2/r

velocity at point 2 = sqrt(2*(-9.8^2/6.4)*(-12)) = 18.98 m/s

What equation are you using here?

2) velocity at point 3 = sqrt(-2*(9.8)(4.5)+18.98^2) = 16.49 m/s

correct your value for the speed at point 2.

 

[dvep]

What equation are you using here? correct your value for the speed at point 2.

I'm using the equation vf-vi = 2ad, but for the acceleration a I used the centripetal acceleration ac = v^2/r

Is that wrong then?

So for 2) if my velocity at point 3 is correct, how do I calculate the minimum radius if it is not the value that is equal to gravity?

 

[PhanthomJay]

This is wrong. Don't use the kinematic equations of motion with constant acceleration for problems such as this where both the tangential and radial acceleratiions are far from being constant. Are you familiar with conservation of energy to solve for the speeds? Once you get them, then you can use your centripetal force equation to solve for the curvature radius at point 3.

 

[dvep]

This is wrong. Don't use the kinematic equations of motion with constant acceleration for problems such as this where both the tangential and radial acceleratiions are far from being constant. Are you familiar with conservation of energy to solve for the speeds? Once you get them, then you can use your centripetal force equation to solve for the curvature radius at point 3.

Thank you for your replies.
How would I use the conservation of energy to solve it?
Also you said the velocity I put down was correct at point 2, but I'm unsure how this is as the initial velocity is 0.

 

[PhanthomJay]

Thank you for your replies.
How would I use the conservation of energy to solve it?

For situations (such as this example) where no work is done by non conservative forces, then the sum of the kinetic and potential energies at any point is always the same.

Also you said the velocity I put down was correct at point 2, but I'm unsure how this is as the initial velocity is 0.

I did not say it was correct...your relevant equation for the normal force is correct, but your calc for the speed to use in that equation was incorrect.

 

[dvep]

For situations (such as this example) where no work is done by non conservative forces, then the sum of the kinetic and potential energies at any point is always the same. I did not say it was correct...your relevant equation for the normal force is correct, but your calc for the speed to use in that equation was incorrect.

Ok, so now I got:

at point 2: PE=0 J, KE=152880 J
velocity at point 2 = sqrt(2KE/m)= 15.336 m/s

at point 3: PE=57330 J, KE=95550 J
velocity at point 3 =sqrt(sKE/m)= 12.124 m/s

normal force at point 2 = mv^2/r +mg= 60513.557 N

and for the radius r=mv^2/mg = v^2/g = 14.999 m

am i on the right track?

 

[PhanthomJay]

Ok, so now I got:

at point 2: PE=0 J, KE=152880 J
velocity at point 2 = sqrt(2KE/m)= 15.336 m/s

at point 3: PE=57330 J, KE=95550 J
velocity at point 3 =sqrt(sKE/m)= 12.124 m/s

normal force at point 2 = mv^2/r +mg= 60513.557 N

and for the radius r=mv^2/mg = v^2/g = 14.999 m

am i on the right track?

Very much so. Your answers now appear correct. Just be sure to round them off to reasonable values (2 significant figures or so).

 

[dvep]

Very much so. Your answers now appear correct. Just be sure to round them off to reasonable values (2 significant figures or so).

Thank you for your help