cyberdiver said:
So I look at the Minowski diagrams, and I can understand that moving on the y means moving in time, and moving on the x means moving in space, but drawing some diagrams of my own, I find it impossible to see why it would imply FTL travel. All objects travel either directly on the x (instantaneous jump) or forwards. I can understand why you would have some weird visual effects (seeing yourself jump into hyperspace after the jump), but I cannot understand why it would imply time travel, and have given up all attempts to interpret the Minowski diagrams.
Could anyone help by explaining exactly what would happen if a spaceship was equipped with an FTL jump drive?
First, let's prove a little theorem:
Theorem 1: If FTL travel is possible in every frame, then instantaneous travel is possible.
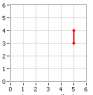
To see this, let an FTL rocket travel from the point x=0, t=0 to the point x=L, t=L/w, where w is the speed of the FTL rocket. Now, switch to another frame using the Lorentz transforms.
(x=0, t=0) \rightarrow (x'=0, t'=0)
(x=L, t=L/w) \rightarrow (x'=\gamma L (1-v/w), t' = \gamma L/w (1 - vw/c^2))
Now, if we choose v = c^2/w, then we have the rocket arriving at time
t'=0 in the primed frame. So in the primed frame, the rocket arrives instantaneously.
So FTL travel in one frame implies instantaneous travel in a different frame. If instantaneous travel is possible in one frame, then it is possible in every frame, by the relativity principle.
Theorem 2: If instantaneous travel is possible in every frame, then back-in-time travel is possible.
To see this, just pick any two frames, F and F' with a relative (slower-than-light) speed v.
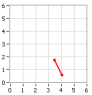
Send a rocket instantaneously according to frame F from
x=0 at time t=0 to x=L at time t=0.
According to frame F', the rocket left at time t'=0 and arrived at time t'=- \gamma vL/c^2. Now, send the rocket back to the point x=0 instantaneously according to frame F'. The rocket arrives at time t'=- \gamma vL/c^2. Using the Lorentz transforms again, we see that:
t' = \gamma (t - vx/c^2) = \gamma t
So t = t'/\gamma = - vL/c^2
So the rocket gets back at a time
BEFORE time t=0.