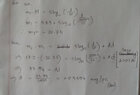How Far is Nanyang's Star from Earth in Parsecs?

In summary, star magnitude is a measure of the brightness of a star as seen from Earth, and it is measured on a logarithmic scale. It can change due to various factors such as distance, luminosity, and intervening objects. There are two types of magnitude: apparent and absolute, which measure how bright a star appears from Earth and at a standard distance of 10 parsecs, respectively. Studying star magnitude is crucial for understanding the properties and evolution of stars, as well as their role in the universe and other celestial objects.
  • #1
Scripturient
1
1
Homework Statement
Suppose that to a particular heliocentric 3D-Cartesian coordinate, the Earth is located at (1,0,0) A.U. You tried to observe Nanyang Star (with the same luminosity as the Sun) from the Earth. Nanyang Star is located at (1,0,1) kpc in the same coordinate system. If you obtained a visual magnitude of +17.2 from the observation, what is the coefficient of absorption, defined as the visual magnitude increase per unit distance due to interstellar matter, in the star’s direction? (It is given that Sun’s absolute magnitude is +4.83.)
Relevant Equations
Apparent Magnitude
73341974-82DB-4DE5-8B66-247B5D291A10.jpegMy attempt has been attached.
 
  • Like
Likes Delta2
Physics news on Phys.org
  • #2
Shouldn't you have m2 - m1 = 5log(d2/d1) + Ad2?
And is d2 = 1000 pc?
 
  • #3
As @mjc123 implied, you don't have d specified correctly. How far is it from Earth to Nanyang's star in pc? This is what you should use for d.
 

FAQ: How Far is Nanyang's Star from Earth in Parsecs?

What is star magnitude?

Star magnitude is a measure of the brightness of a star as seen from Earth. It is a logarithmic scale, meaning that a difference of 1 magnitude represents a difference of approximately 2.5 times in brightness.

How is star magnitude measured?

Star magnitude is measured using a device called a photometer, which measures the amount of light emitted by a star. The magnitude scale was originally developed by the ancient Greek astronomer Hipparchus, who divided stars into six categories based on their apparent brightness.

What is the difference between apparent and absolute magnitude?

Apparent magnitude is a measure of how bright a star appears from Earth, while absolute magnitude is a measure of how bright a star would appear if it were located 10 parsecs (32.6 light years) away from Earth. Absolute magnitude takes into account a star's intrinsic brightness, while apparent magnitude is affected by its distance from Earth.

What is the brightest star in the night sky?

The brightest star in the night sky is Sirius, also known as the "Dog Star." It has an apparent magnitude of -1.46, making it almost twice as bright as the next brightest star, Canopus.

Can star magnitude change over time?

Yes, star magnitude can change over time due to a variety of factors such as changes in a star's brightness, its distance from Earth, and any objects that may be blocking its light. This is why astronomers regularly measure and monitor the magnitude of stars to track any changes or variations.

Similar threads

B What is a parsec and how is it measured?
Replies
7
Views
2K
Calculating distance to a star using magnitudes
Replies
1
Views
2K
Solve Obler's Paradox: Calculate Universe Size in Parsecs & Light Years
Replies
1
Views
1K
Numerically simulating stellar pulsation using a "one zone" model
Replies
1
Views
1K
Measure the distance to a star using magnitude and extinction
Replies
8
Views
1K
How do I determine the uncertainty value of the star's absolute magnitude?
Replies
6
Views
2K
Color Indices and Absolute and Apparent Bolometric Magnitude
Replies
4
Views
2K
B Star visible for longest time from Earth
Replies
6
Views
1K
Astrophysics Questions: Calculating Distances, Intensities, and Magnitudes
Replies
4
Views
7K
I Correlation between a Star's Luminosity and Distance?
Replies
10
Views
3K

Hot Threads

Recent Insights

Back
Top