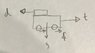
You have 2 resistances: rolling resistance ##F_R## and aerodynamic drag ##F_D##. Aerodynamic drag should be the greatest by far.To get the acceleration, it is simply:
$$\sum F = ma$$
$$F - F_R - F_D = ma$$
$$a = \frac{F - F_R - F_D}{m}$$
Where ##F## is the force produced by your rocket.
During the travel time, these forces will vary, so the acceleration will also vary. For the rocket, I'm not an expert on these engines so I can only guess on the force output versus time ##F(t)## equation to define it. Maybe other can chime in. But let's imagine that it is constant for the full 1 s.
The rolling resistance is mathematically similar to friction, so ##F_R = C_{rr} F_N##, where ##C_{rr}## is the
coefficient of rolling resistance and ##F_N## is the normal force (i.e. the vehicle weight ##mg## in our case).
The aerodynamic drag is ##F_D = \frac{1}{2}\rho C_D A_f v^2## where ##\rho## is the air density (1.23 kg/m³), ##C_D## is the
drag coefficient and ##A_f## is the frontal area of the vehicle and v is the speed of the vehicle. As you can see, as the vehicle increase in speed, the drag increases, thus your acceleration will get smaller as it travels.
To calculate the velocity after 1 s of travel (when the rocket pushes the vehicle):
$$dv = adt$$
$$dv = \frac{F - C_{rr} F_N - \frac{1}{2}\rho C_D A_f v^2}{m}dt$$
Which can be rewritten as:
$$\frac{dv}{\frac{F}{m} - C_{rr} g - \frac{\rho C_D A_f}{2m}v^2} = dt$$
Simplified as:
$$-\frac{1}{B}\frac{dv}{v^2 - C^2} = dt$$
or
$$t = -\frac{1}{B}\int_0^{v_f}{\frac{dv}{v^2 - C^2}}$$
Where:
##A = \frac{F}{m} - C_{rr} g##;
##B = \frac{\rho C_D A_f}{2m}##;
##C = \sqrt{\frac{A}{B}}##.
The
solution of the previous integral is:
$$t = -\frac{1}{2CB}\ln\left|\frac{v_f-C}{v_f+C}\right|$$
You can find ##v_f## for ##t=1## by trial and error. Check that ##a(v_f) > 0##. If it is not, then calculate the speed ##v_f## that will give you ##a = 0## and find times ##t'## that it will take to reach that speed with the previous equation. Then the vehicle will be going at constant speed ##v_f##. ##v_f## when ##a=0## is known as the
terminal velocity of your vehicle.
After you found ##v_f## (and ##t'## if that was the case), you can find the distance traveled with:
$$dx = \frac{v}{a}dv$$
$$dx = \frac{v}{\frac{F}{m} - C_{rr} g - \frac{\rho C_D A_f}{2m}v^2}dv$$
Simplified as:
$$dx = \frac{v}{-Bv^2+ A}dv$$
or
$$x = \int_{v_0}^{v_f}{\frac{v}{-Bv^2+ A}dv}$$
The solution to this integral (
see 17 here) is:
$$x = \frac{\ln\left|-Bv_f^2+A\right|}{-2B} - \frac{\ln\left|-Bv_0^2+A\right|}{-2B}$$
Where ##v_f## was found previously and ##v_0## would be the initial velocity, i.e. 0.
If there was a ##t'## found previously, the vehicle will travel from ##t'## to ##t## at constant speed ##v_f##, thus you must add ##v_f (t- t')## to ##x## to find the total distance traveled during the full time ##t##.
The rocket stops
Now your vehicle is going at speed ##v_f## and has traveled a distance ##x## after time ##t=1\ s## (or whatever other time you want). The rocket stops pushing, thus ##F=0## at this point and ##A## is modified to ##A' = - C_{rr} g##. What we want to know is how far will it go before it stops by itself (due to drag and rolling resistance).
We know the initial speed ##v_f## at this point and we know final speed will be 0 when it stops. Thus we can use the same equation as before, but with the new values:
$$x' = \frac{\ln\left|-B(0)^2+A'\right|}{-2B} - \frac{\ln\left|-Bv_f^2+A'\right|}{-2B}$$
And the total distance ##d## traveled will be:
$$d = x+x'$$
Test
With the following data:
##m = 0.3\ kg##;
##F = 10\ N##;
##C_{RR} = 0.01##;
##C_D = 0.4##;
##A_f = 0.1\ m \times 0.1\ m##.
I get for ##t=1\ s##:
##v_f = 30.5\ m/s##;
##x = 15.9\ m##;
##d = 282.2\ m##.
If there is a discrepancy between those numbers and my equations, there is probably an error in my equations when I transcribed them.